某学校共有师生2400人,现用分层抽样的方法,从所有师生中抽取一个容量为150的样本,已知从学生中抽取的人数为135,那么该学校的教师人数是( )
| A.15 | B.200 | C.240 | D.2160 |
为了解某校高三学生的视力情况,随机地
抽查了该校100名高三学生的视力情况,
得到频率分布直方图,如右,由于不慎将
部分数据丢失,但知道前4组的频数成等
比数列,后6组的频数成等差数列,设最
大频率为a,视力在4.6到5.0之间的
学生数为b,则a, b的值分别为( )
| A.0.27, 78 | B.0.27, 83 |
| C.2.7, 78 | D.2.7, 83 |
 |
经销商经销某种农产品,在一个销售季度内,每售出 t该产品获利润
t该产品获利润 元,未售出的产品,每
元,未售出的产品,每 t亏损
t亏损 元。根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示。经销商为下一个销售季度购进了
元。根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示。经销商为下一个销售季度购进了 t该农产品,以
t该农产品,以 (单位:t,
(单位:t, )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量, (单位:元)表示下一个销售季度内销商该农产品的利润。
(单位:元)表示下一个销售季度内销商该农产品的利润。
(1)将 表示为
表示为 的函数;(2)根据直方图估计利润
的函数;(2)根据直方图估计利润 不少于57000元的概率.
不少于57000元的概率.
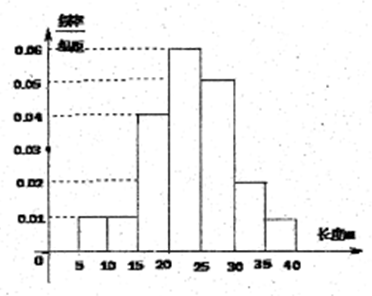
某棉纺厂为了了解一批棉花的质量,从中随机抽取了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标),所得数据都在区间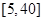 中,其频率分布直方图如图所示,则其抽样的100根中,有 根在棉花纤维的长度大于25mm.
中,其频率分布直方图如图所示,则其抽样的100根中,有 根在棉花纤维的长度大于25mm.
统计某校1000名学生的数学会考成绩,得到样本频率分布直方图如右图所示,规定不低于60分为及格,则及格人数是 。
由某种设备的使用年限 (年)与所支出的维修费
(年)与所支出的维修费 (万元)的数据资料,算得
(万元)的数据资料,算得 ,
, ,
, ,
,  .
.
(Ⅰ)求所支出的维修费 对使用年限
对使用年限 的线性回归方程
的线性回归方程 ;
;
(Ⅱ)判断变量 与
与 之间是正相关还是负相关;
之间是正相关还是负相关;
(Ⅲ)估计使用年限为8年时,支出的维修费约是多少.
附:在线性回归方程 中,
中, ,
, ,其中
,其中 ,
, 为
为
样本平均值,线性回归方程也可写为 .
.
(本小题满分12分)从某学校高三年级共800名男生中随机抽取50名测量身高,据测量被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组 、第二组
、第二组 ;…第八组
;…第八组 ,右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
,右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
(I)求第六组、第七组的频率并补充完整频率分布直方图;
(II)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为 ,求满足
,求满足 的事件概率;
的事件概率;
(III)从最后三组中任取3名学生参加学校篮球队,用 表示从第八组中取到的人数,求
表示从第八组中取到的人数,求 的分布列及其数学期望。
的分布列及其数学期望。
(本小题满分12分)某校为了响应《中共中央国务院关于加强青少年体育增强青少年体质的意见》精神,落实“生命—和谐”教育理念和阳光体育行动的现代健康理念,学校特组织“踢毽球”大赛,某班为了选出一人参加比赛,对班上甲乙两位同学进行了 次测试,且每次测试之间是相互独立.成绩如下:(单位:个/分钟)
次测试,且每次测试之间是相互独立.成绩如下:(单位:个/分钟)
| 甲 |
80 |
81 |
93 |
72 |
88 |
75 |
83 |
84 |
| 乙 |
82 |
93 |
70 |
84 |
77 |
87 |
78 |
85 |
(1)用茎叶图表示这两组数据
(2)从统计学的角度考虑,你认为选派那位学生参加比赛合适,请说明理由?
(3)若将频率视为概率,对甲同学在今后的三次比赛成绩进行预测,记这三次成绩高于 个/分钟的次数为
个/分钟的次数为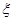 ,求
,求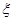 的分布列及数学期望
的分布列及数学期望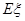 .
.
(参考数据: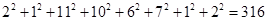 ,
,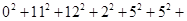
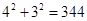 )
)
成都市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的则被淘汰。若现有500人参加测试,学生成绩的频率分布直方图如下:
(I)求获得参赛资格的人数;
(II)根据频率直方图,估算这500名学生测试的平均成绩;
(III)若知识竞赛分初赛和复赛,在初赛中每人最多有5次选题答题的机会,累计答对3题或答错3题即终止,答对3题者方可参加复赛,已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响,已知他连续两次答错的概率为 ,求甲在初赛中答题个数的分布列及数学期望.
,求甲在初赛中答题个数的分布列及数学期望.
利用随机数表法对一个容量为500编号为000,001,002,…,499的产品进行抽样检验,抽取一个容量为10的样本,若选定从第12行第4列的数开始向右读数,(下面摘取了随机数表中的第11行至第15行),根据下图,读出的第3个数是( )

| A.584 | B.114 | C.311 | D.160 |
为了了解小学五年级学生的体能情况,抽取了实验小学五年级部分学生进行踢毽子测试,将所得的数据整理后画出频率分布直方图(如图),已知图中从左到右的前三个小组的频率分别是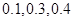 ,第一小组的频数是
,第一小组的频数是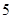 .
.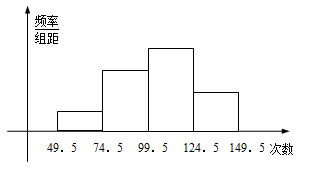
(Ⅰ)求第四小组的频率和参加这次测试的学生人数;
(Ⅱ)在这次测试中,问学生踢毽子次数的中位数落在第几小组内?
(Ⅲ)在这次跳绳测试中,规定跳绳次数在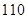 以上的为优秀,试估计该校此年级跳绳成绩的优秀率是多
以上的为优秀,试估计该校此年级跳绳成绩的优秀率是多
少?
(本小题满分12分)贵阳市某中学高三第一次摸底考试中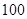 名学生数学成绩的频率分布直方图如图
名学生数学成绩的频率分布直方图如图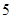 所示,其中成绩分组区间是
所示,其中成绩分组区间是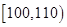 ,
,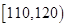 ,
,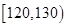 ,
, ,
,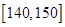 .
.
(Ⅰ)求图中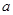 的值;
的值;
(Ⅱ)根据频率分布直方图,估计这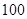 名学生数学成绩的平均分;
名学生数学成绩的平均分;
(Ⅲ)若这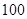 名学生数学成绩某些分数段的人数(
名学生数学成绩某些分数段的人数( )与语文成绩相应分数段的人数(
)与语文成绩相应分数段的人数(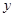 )之比如下表所示,求语文成绩在
)之比如下表所示,求语文成绩在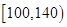 之外的人数.
之外的人数.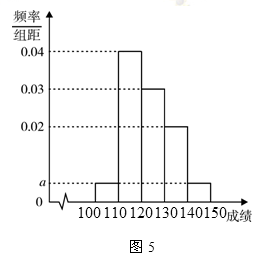

某服装商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某3个月的月销售量与当月平均气温,其数据如下表:
月平均气温 (°C) (°C) |
11 |
13 |
12 |
| 月销售量y(件) |
25 |
30 |
26 |
由表中数据能算出线性回归方程为 .(参考公式: )
)
某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
| 分数段 |
[50,70) |
[70,90) |
[90,110) |
[110,130) |
[130,150) |
总计 |
| 频数 |
|
|
|
b |
|
|
| 频率 |
a |
0.25 |
|
|
|
|

(1)求表中a,b的值及分数在[90,100)范围内的学生人数,并估计这次考试全校学生数学成绩的及格率(分数在[90,150)内为及格):
(2)从成绩在[100,130)范围内的学生中随机选4人,
设其中成绩在[100,110)内的人数为X,求X的分布列及数学期望.
试题篮
()