高中数学平行线法试题

如果直线平行于平面，则（    ）．

A．平面内有且只有一直线与平行	B．平面内有无数条直线与平行
C．平面内不存在与垂直的直线	D．平面内有且仅有一条与垂直的直线

能保证直线与平面平行的条件是（   ）．

A．直线与平面内的一条直线平行

B．直线与平面内的某条直线不相交

C．直线与平面内的无数条直线平行

D．直线与平面内的所有直线不相交

下列命题正确的是（   ）．                                        

A．	B．
C．	D．

已知长方体．
（1）求证：平面；
（2）若、分别是的中点，则平面．

如图，四棱锥S- ABCD中，底面ABCD为平行四边形，E是SA上一点，试探求点E的位置，使SC//平面EBD，并证明．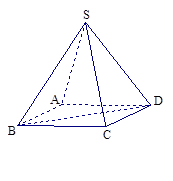

答：点E的位置是                        ．
证明：

.若三个平面两两相交，且三条交线互相平行，
则这三个平面把空间分成（ ）

A．5部分

B．6部分

C．7部分

D．8部分

.如图，ABCD-A₁B₁C₁D₁是棱长为的正方体，M，N，P，Q，R，S分别是AA₁，AB，AD，CC₁，B₁C₁，C₁D₁的中点，求证：平面PMN∥平面QRS。

下列条件中，能判定平面∥平面的是(        ).

A．存在两条相交直线分别与，成等角

B．内有不在同一条直线上的三个点到的距离相等

C．内有△ABC与内△A1B1C1全等，且有AA1∥BB1∥CC1

D．，都与异面直线a,b平行

如图：在三棱锥中，已知点、、分别为棱、、的中点.①求证：∥平面.②若，，求证：平面⊥平面 .

如图所示，四棱锥P－ABCD中，底面ABCD是矩形，PA⊥平面ABCD，M、N分别是AB、PC的中点，PA＝AD＝a．
（1）求证：MN∥平面PAD；
（2）求证：平面PMC⊥平面PCD．

如图所示，正方体ABCD－A₁B₁C₁D₁中，E、F分别是AB、BC的中点，G为DD₁上一点，且D₁G：GD＝1：2，AC∩BD＝O，求证：平面AGO//平面D₁EF．

 

 

如图所示，三个平面两两相交，有三条交线，求证这三条交线交于一点或互相平行．

.设表示不同的直线，表示不同的平面，给出下列4个命题：
①若，且，则；
②若，且∥，则；
③若，则；
④若，且，则.
其中正确命题的个数是                                                   

A．1

B．2

C．3

D．4

已知：AB、BC、CD是不在同一平面内的三条线段，E、F、G分别为AB、BC、CD的中点. 求证：AC//平面EFG, BD//平面EFG.

在△ABC所在平面外有一点P，M、N分别是PC和AC上的点，过MN作平面平行于BC，画出这个平面与其他各面的交线，并说明画法的理由。