为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| |
喜爱打篮球 |
不喜爱打篮球 |
合计 |
| 男生 |
|
5 |
|
| 女生 |
10 |
|
|
| 合计 |
|
|
50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为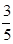 .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;
(3)已知喜爱打篮球的10位女生中,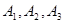 还喜欢打羽毛球,
还喜欢打羽毛球,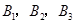 还喜欢打乒乓球,
还喜欢打乒乓球,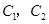 还喜欢踢足球,现在从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的8位女生中各选出1名进行其他方面的调查,求
还喜欢踢足球,现在从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的8位女生中各选出1名进行其他方面的调查,求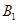 和
和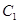 不全被选中的概率.
不全被选中的概率.
下面的临界值表供参考:
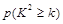 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
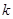 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: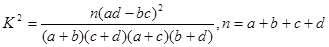 )
)
随机观测生产某种零件的某工厂 名工人的日加工零件数(单位:件),获得数据如下:
名工人的日加工零件数(单位:件),获得数据如下: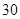 、
、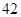 、
、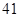 、
、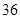 、
、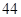 、
、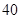 、
、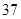 、
、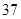 、
、 、
、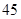 、
、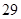 、
、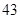 、
、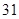 、
、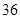 、
、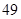 、
、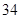 、
、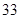 、
、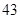 、
、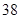 、
、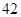 、
、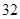 、
、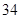 、
、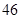 、
、 、
、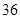 ,根据上述数据得到样本的频率分布表如下:
,根据上述数据得到样本的频率分布表如下:
| 分组 |
频数 |
频率 |
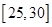 |
 |
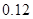 |
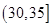 |
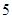 |
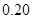 |
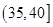 |
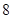 |
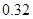 |
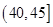 |
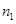 |
|
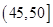 |
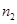 |
(1)确定样本频率分布表中的值;
(2)根据上述频率分布表,画出样本频率分布直方图;
(3)根据样本频率分布直方图,求在该厂任取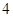 人,至少有
人,至少有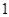 人的日加工零件数落在区间
人的日加工零件数落在区间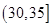 的概率.
的概率.
江西某品牌豆腐食品是经过 、
、 、
、 三道工序加工而成的,
三道工序加工而成的, 、
、 、
、 工序的产品合格率分别为
工序的产品合格率分别为 、
、 、
、 .已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;恰有两次合格为二等品;其它的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;恰有两次合格为二等品;其它的为废品,不进入市场.
(1)生产一袋豆腐食品,求产品为废品的概率;
(2)生产一袋豆腐食品,设 为三道加工工序中产品合格的工序数,求
为三道加工工序中产品合格的工序数,求 的分布列和数学期望.
的分布列和数学期望.
一个袋子中装有6个红球和4个白球,假设袋子中的每一个球被摸到可能性是相等的。
(Ⅰ)从袋子中任意摸出3个球,求摸出的球均为白球的概率;
(Ⅱ)一次从袋子中任意摸出3个球,若其中红球的个数多于白球的个数,则称“摸球成功”(每次操作完成后将球放回),某人连续摸了3次,记“摸球成功”的次数为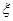 ,求
,求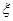 的分布列和数学期望。
的分布列和数学期望。
在某校高三学生的数学校本课程选课过程中,规定每位同学只能选一个科目.已知某班第一小组与第二小组各有六位同学选择科目甲或科目乙,情况如下表:
| |
科目甲 |
科目乙 |
总计 |
| 第一小组 |
1 |
5 |
6 |
| 第二小组 |
2 |
4 |
6 |
| 总计 |
3 |
9 |
12 |
现从第一小组、第二小组中各任选2人分析选课情况.
(1)求选出的4人均选科目乙的概率;
(2)设 为选出的4个人中选科目甲的人数,求
为选出的4个人中选科目甲的人数,求 的分布列和数学期望.
的分布列和数学期望.
老师要从10篇课文中随机抽3篇让学生背诵,规定至少要背出其中2篇才能及格.某同学只能背诵其中的6篇,试求:
(1)抽到他能背诵的课文的数量的分布列;
(2)他能及格的概率.
若盒中装有同一型号的灯泡共 只,其中有
只,其中有 只合格品,
只合格品, 只次品。
只次品。
(1) 某工人师傅有放回地连续从该盒中取灯泡 次,每次取一只灯泡,求
次,每次取一只灯泡,求 次取到次品的概率;
次取到次品的概率;
(2) 某工人师傅用该盒中的灯泡去更换会议室的一只已坏灯泡,每次从中取一灯泡,若是正品则用它更换已坏灯泡,若是次品则将其报废(不再放回原盒中),求成功更换会议室的已坏灯泡所用灯泡只数 的分布列和数学期望.
的分布列和数学期望.
为考察某种药物预防禽流感的效果,进行动物家禽试验,调查了100个样本,统计结果为:服用药的共有60个样本,服用药但患病的仍有20个样本,没有服用药且未患病的有20个样本.
(1)根据所给样本数据完成下面2×2列联表;
(2)请问能有多大把握认为药物有效?
| |
不得禽流感 |
得禽流感 |
总计 |
| 服药 |
|
|
|
| 不服药 |
|
|
|
| 总计 |
|
|
|
某电视台综艺频道组织的闯关游戏,游戏规定前两关至少过一关才有资格闯第三关,闯关者闯第一关成功得3分,闯第二关成功得3分,闯第三关成功得4分.现有一位参加游戏者单独面第一关、第二关、第三关成功的概率分别为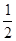 ,
,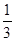 ,
,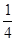 ,记该参加者闯三关所得总分为ζ.
,记该参加者闯三关所得总分为ζ.
(1)求该参加者有资格闯第三关的概率;
(2)求ζ的分布列和数学期望.
某篮球队与其他6支篮球队依次进行6场比赛,每场均决出胜负,设这支篮球队与其他篮球队比赛胜场的事件是独立的,并且胜场的概率是 .
.
(1)求这支篮球队首次胜场前已经负了两场的概率;
(2)求这支篮球队在6场比赛中恰好胜了3场的概率;
(3)求这支篮球队在6场比赛中胜场数的期望和方差.
甲、乙两人独立地破译1个密码,他们能译出密码的概率分别为 和
和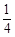 ,求
,求
(1)恰有1人译出密码的概率;
(2)若达到译出密码的概率为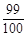 ,至少需要多少乙这样的人.
,至少需要多少乙这样的人.
在乒乓球比赛中,甲与乙以“五局三胜”制进行比赛,根据以往比赛情况,甲在每一局胜乙的概率均为 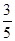 .已知比赛中,乙先赢了第一局,求:
.已知比赛中,乙先赢了第一局,求:
(Ⅰ)甲在这种情况下取胜的概率;
(Ⅱ)设比赛局数为X,求X的分布列及数学期望(均用分数作答)。
为了解某班关注NBA(美国职业篮球)是否与性别有关,对某班48人进行了问卷调查得到如下的列联表:
| |
关注NBA |
不关注NBA |
合计 |
| 男生 |
|
6 |
|
| 女生 |
10 |
|
|
| 合计 |
|
|
48 |
已知在全班48人中随机抽取1人,抽到关注NBA的学生的概率为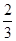 .
.
(1)请将上面的表补充完整(不用写计算过程),并判断是否有95%的把握认为关注NBA与性别有关?说明你的理由;
(2)设甲,乙是不关注NBA的6名男生中的两人,丙,丁,戊是关注NBA的10名女生中的3人,从这5人中选取2人进行调查,求:甲,乙至少有一人被选中的概率.
答题参考
| P(K2≥k) |
0.10 |
0.05 |
0.010 |
0.005 |
| k0 |
2.706 |
3.841 |
6.635 |
7.879 |
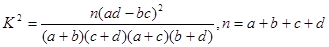
为了解心肺疾病是否与年龄相关,现随机抽取了40名市民,得到数据如下表:
| |
患心肺疾病 |
不患心肺疾病 |
合计 |
| 大于40岁 |
16 |
|
|
| 小于等于40岁 |
|
12 |
|
| 合计 |
|
|
40 |
已知在全部的40人中随机抽取1人,抽到不患心肺疾病的概率为
(1)请将 列联表补充完整;
列联表补充完整;
(2)已知大于40岁患心肺疾病市民中,经检查其中有4名重症患者,专家建议重症患者住院治疗,现从这16名患者中选出两名,记需住院治疗的人数为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(3)能否在犯错误的概率不超过0.01的前提下认为患心肺疾病与年龄有关?
下面的临界值表供参考:
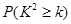 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: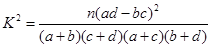 ,其中
,其中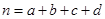 )
)
试题篮
()