高中数学正交试验设计方法试题

（本小题共13分）某市医疗保险实行定点医疗制度，按照“就近就医、方便管理”的原则，参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为本人就诊的医疗机构．若甲、乙、丙、丁4名参加保险人员所在地区附近有A，B，C三家社区医院，并且他们的选择是相互独立的．
（Ⅰ）求甲、乙两人都选择A社区医院的概率；
（Ⅱ）求甲、乙两人不选择同一家社区医院的概率；
（Ⅲ）设4名参加保险人员中选择A社区医院的人数为ξ，求ξ的分布列和数学期望．

掷两颗骰子，所得点数之和为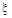，那么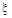=4表示的随机试验结果是（  ）

A．一颗是3点，一颗是1点	B．两颗都是2点
C．两颗都是4点	D．一颗是3点，一颗是1点或两颗都是2点

在某校举办的元旦有奖知识问答中，甲、乙、丙三人同时回答一道有关环保知识的问题，已知甲回答对这道题的概率是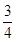，甲、丙两人都回答错的概率是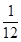，乙、丙两人都回答对的概率是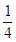.(Ⅰ)求乙、丙两人各自回答对这道题的概率；(Ⅱ)用表示回答对该题的人数，求的分布列和数学期望E.

甲、乙两队在进行一场五局三胜制的排球比赛中，规定先赢三局的队获胜，并且比赛就此结束，现已知甲、乙两队每比赛一局，甲队获胜的概率为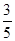，乙队获胜的概率为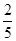，且每局比赛的胜负是相互独立的，问：
（1）甲队以获胜的概率是多少？
（2）乙队获胜的概率是多少？

在吸烟与患肺病这两个分类变量的计算中，下列说法正确的是(　　)
①若K²的观测值满足K²≥6.635，我们有99%的把握认为吸烟与患肺病有关系，那么在100个吸烟的人中必有99人患有肺病；②从独立性检验可知有99%的把握认为吸烟与患病有关系时，我们说某人吸烟，那么他有99%的可能患有肺病；③从统计量中得知有95%的把握认为吸烟与患肺病有关系，是指有5%的可能性使得推断出现错误

A．①

B．①③

C．③

D．②

根据以往统计资料，某地车主购买甲种保险的概率为0.5，购买乙种保险但不购买甲种保险的概率为0.3。设各车主购买保险相互独立.
（Ⅰ）求该地1位车主至少购买甲、乙两种保险中的1种的概率；
（Ⅱ）求该地3位车主中恰有1位车主甲、乙两种保险都不购买的概率.

已知随机变量ξ的概率分布如下：

ξ	1	2	3	4	5	6	7	8	9	10
P										m

则P(ξ＝10)等于(　　)
A、           B、        C、         D.、

已知随机变量，且，则p和n的值依次为(   )

A．，36

B．，18

C．，72

D．，24

(本题满分12分)有朋自远方来，他乘火车、轮船、汽车、飞机来的概率分别为0.3,0.2,0.1,0.4.
试问：(1)他乘火车或乘飞机来的概率；
(2)他不乘轮船来的概率；
(3)如果他来的概率为0.5，请问他有可能是乘何种交通工具来的．
即他不乘轮船来的概率为0.8.

甲、乙两篮球运动员在罚球线投球的命中率分别是0.7和0.6，每人投球3次，则两人都投进2球的概率是_______

甲、乙、丙三人进行乒乓球练习赛，其中两人比赛，另一人当裁判，每局比赛结束时，负的一方在下一局当裁判．设各局中双方获胜的概率均为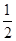，各局比赛的结果相互独立，第1局甲当裁判．
（1）求第4局甲当裁判的概率；
（2）用X表示前4局中乙当裁判的次数，求X的分布列和数学期望．

为了解某市市民对政府出台楼市限购令的态度，在该市随机抽取了50名市民进行调查，他们月收入（单位：百元）的频数分布及对楼市限购令的赞成人数如下表：

月收入		[25，35）	[35，45）
频数	5	10	15	10	5	5
赞成人数	4	8	8	5	2	1

将月收入不低于55的人群称为“高收入族”，月收入低于55的人群称为“非高收人族”。
（Ⅰ）根据已知条件完成下面的2×2列联表，有多大的把握认为赞不赞成楼市限购令与收入高低有关？
已知：，
当<2.706时，没有充分的证据判定赞不赞成楼市限购令与收入高低有关；
当>2.706时，有90％的把握判定赞不赞成楼市限购令与收入高低有关；
当>3.841时，有95％的把握判定赞不赞成楼市限购令与收入高低有关；
当>6.635时，有99％的把握判定赞不赞成楼市限购令与收入高低有关。

	非高收入族	高收入族	总计
赞成
不赞成
总计

（Ⅱ）现从月收入在[55，65）的人群中随机抽取两人，求所抽取的两人中至少一人赞成楼市限购令的概率。

设随机变量X服从二项分布，即X～B(n，p)，且E(X)＝3，p＝，则n＝________，V(X)＝________.

某中学经市批准建设分校，工程从2010年底开工到2013年底完工，分三期完成，经过初步招标淘汰后，确定由甲、乙两建筑公司承建，且每期工程由两公司之一独立完成，必须在建完前一期工程后再建后一期工程，已知甲公司获得第一期，第二期，第三期工程承包权的概率分别是，，．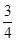
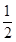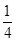(I)求甲乙两公司均至少获得l期工程的概率；
(II)求甲公司获得的工程期数的分布列和数学期望E(X)．

(8分)一个口袋有5个同样大小的球，编号为1、2、3、4、5，从中同时取出3个，以ξ表示取出球编号的最小号码，求(1)ξ的分布列．(2)取出球编号最小的号码小于等于2的概率