如图,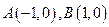 ,过曲线
,过曲线 上一点
上一点 的切线
的切线 ,与曲线
,与曲线 也相切于点
也相切于点 ,记点
,记点 的横坐标为
的横坐标为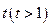 。
。
(1)用 表示切线
表示切线 的方程;
的方程;
(2)用 表示
表示 的值和点
的值和点 的坐标;
的坐标;
(3)当实数 取何值时,
取何值时, ?
?
并求此时 所在直线的方程。
所在直线的方程。
(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,已知曲线 ,将
,将 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的 、2倍后得到曲线
、2倍后得到曲线 . 以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
. 以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线 .
.
(Ⅰ)试写出直线 的直角坐标方程和曲线
的直角坐标方程和曲线 的参数方程;
的参数方程;
(Ⅱ)在曲线 上求一点P,使点P到直线
上求一点P,使点P到直线 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
(本小题满分10分)选修4-1:几何证明选讲
如图所示,AB是⊙O的直径,
G为AB延长线上的一点,GCD是⊙O的割线,过点
G作AB的垂线,交AC的延长线于点E,交AD的延
长线于点F,过G作⊙O的切线,切点为H .
求证:(Ⅰ)C,D,F,E四点共圆;
(Ⅱ)GH2=GE·GF.
(本小题满分12分)一动圆与已知 :
: 相外切,与
相外切,与 :
: 相内切.
相内切.
(Ⅰ)求动圆圆心的轨迹C;
(Ⅱ)若A(0, 1),轨迹C与直线y="kx+m" (k≠0)相交于不同的两点M、N,当|
1),轨迹C与直线y="kx+m" (k≠0)相交于不同的两点M、N,当| |=|
|=| |时,求m的取值范围.
|时,求m的取值范围.
(本小题满分10分)选修4-1:几何证明选讲
如图所示,AB是⊙O的直径,
G为AB延长线上的一点,GCD是⊙O的割线,过点<
G作AB的垂线,交AC的延长线于点E,交AD的延
长线于点F,过G作⊙O的切线,切点为H .
求证:(Ⅰ)C,D,F,E四点共圆;
(Ⅱ)GH2=GE·GF.
C.(选修4—4:坐标系与参数方程)
若两条曲线的极坐标方程分别为 与
与 ,它们相交于
,它们相交于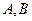 两点,求线段
两点,求线段 的长.
的长.
(本小题满分15分)已知椭圆 的左焦点为F,左右顶点分别为A、C,
的左焦点为F,左右顶点分别为A、C,
上顶点为B,过F,B,C三点作 ,其中圆心P的坐标为
,其中圆心P的坐标为 .
.
(1) 若椭圆的离心率 ,求
,求 的方程;
的方程;
(2)若 的圆心在直线
的圆心在直线 上,求椭圆的方程.
上,求椭圆的方程.
试题篮
()