(本小题满分12分)
已知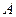 、
、 分别是直线
分别是直线 和
和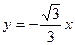 上的两个动点,线段
上的两个动点,线段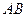 的长为
的长为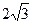 ,
, 是
是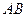 的中点.
的中点.
(1)求动点 的轨迹
的轨迹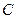 的方程;
的方程;
(2)过点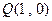 作直线
作直线 (与
(与 轴不垂直)与轨迹
轴不垂直)与轨迹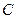 交于
交于 两点,与
两点,与 轴交于点
轴交于点 .若
.若 ,
, ,证明:
,证明: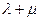 为定值.
为定值.
如图,椭圆
的一个焦点是
,
为坐标原点。
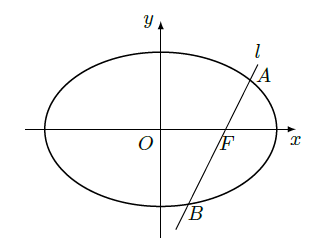
(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程;
(Ⅱ)设过点
的直线
交椭圆于
、
两点,若直线
绕点
任意转动,值有
,求
的取值范围。
双曲线 的两个焦点为 ,若 为其上一点,且 ,则双曲线离心率的取值范围为( )
| A. | (1,3) | B. | (1,3] | C. | (3,+ ) | D. |
已知 是两条不同直线, 是三个不同平面,下列命题中正确的是( )
| A. | 若 ,则 | B. | 若 ,则 |
| C. | 若 ,则 | D. | 若 ,则 |
如图,已知
的两条角平分线
和
相交于
,
,
在
上,且
.
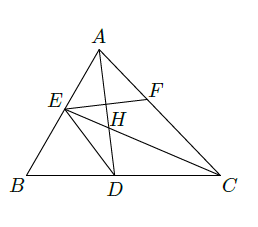
(Ⅰ)证明:
、
、
、
四点共圆;
(Ⅱ)证明:
平分
.
已知平面内两定点 ,动点
,动点 满足条件:
满足条件: ,设点
,设点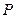 的轨迹是曲线
的轨迹是曲线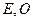 为坐标原点。
为坐标原点。
(I)求曲线 的方程;
的方程;
(II)若直线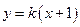 与曲线
与曲线 相交于两不同点
相交于两不同点 ,求
,求 的取值范围;
的取值范围;
(III)(文科做)设 两点分别在直线
两点分别在直线 上,若
上,若 ,记
,记 分别为
分别为 两点的横坐标,求
两点的横坐标,求 的最小值。
的最小值。
(理科做)设 两点分别在直线
两点分别在直线 上,若
上,若 ,求
,求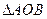 面积的最大值。
面积的最大值。
设抛物线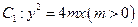 的准线与
的准线与 轴交于点
轴交于点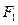 ,焦点为
,焦点为 ;椭圆
;椭圆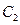 以
以 为焦点,离心率
为焦点,离心率 。
。
(I)当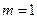 时,①求椭圆
时,①求椭圆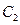 的标准方程;②若直线
的标准方程;②若直线 与抛物线交于
与抛物线交于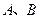 两点,且线段
两点,且线段 恰好被点
恰好被点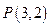 平分,设直线
平分,设直线 与椭圆
与椭圆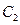 交于
交于 两点,求线段
两点,求线段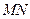 的长;
的长;
(II)(仅理科做)设抛物线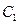 与椭圆
与椭圆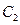 的一个交点为
的一个交点为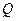 ,是否存在实数
,是否存在实数 ,使得
,使得 的边长是连续的自然数?若存在,求出这样的实数
的边长是连续的自然数?若存在,求出这样的实数 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
试题篮
()