如图,椭圆
的一个焦点是
,
为坐标原点。
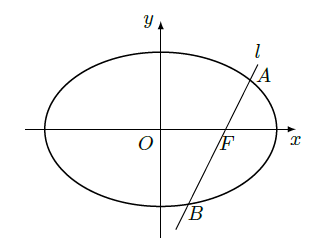
(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程;
(Ⅱ)设过点
的直线
交椭圆于
、
两点,若直线
绕点
任意转动,值有
,求
的取值范围。
(本小题满分13分)
过圆 上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点.
上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)设点P关于点D(9,0)的对称点为E,O为坐标原点,将线段OP绕原点O依逆时针方向旋转90°后,所得线段为OF,求|EF|的取值范围.
(本小题满分13分)
已知动点P到直线 的距离比它到点F
的距离比它到点F 的距离大
的距离大 .
.
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)若点P的轨迹上不存在两点关于直线l: 对称,求实数
对称,求实数 的取值范围.
的取值范围.
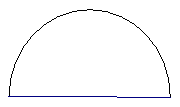
建立适当的坐标系,用坐标法解决下列问题:
已知隧道的截面是半径为4m的半圆,车辆只能在道路中心线一侧行驶,一辆宽为2.7m,高为3m的货车能不能驶入这个隧道?
 |
如图,已知
的两条角平分线
和
相交于
,
,
在
上,且
.
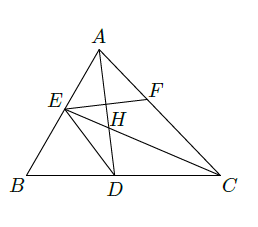
(Ⅰ)证明:
、
、
、
四点共圆;
(Ⅱ)证明:
平分
.
如图,在四边形ABCD中,AD=8,CD=6,AB=13,∠ADC=90°,且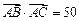 .
.
(1)求sin∠BAD的值;
(2)设△ABD的面积为S△ABD,△BCD的面积为S△BCD,求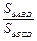 的值.
的值.
 |
如图,F是定直线l外的一个定点,C是l上的动点,有下列结论:若以C为圆心,CF为半径的圆与l交于A、B两点,过A、B分别作l的垂线与圆
C过F的切线交于点P和点Q,则P、Q必在以F为焦点,l为准线的同一条抛物线上.
(Ⅰ)建立适当的坐标系,求出该抛物线的方程;
(Ⅱ)对以上结论的反向思考可以得到另一个命题:
“若过抛物线焦点F的直线与抛物线交于P、Q两点,
则以PQ为直径的圆一定与抛物线的准线l相切”请
问:此命题是否正确?试证明你的判断;
(Ⅲ)请选择椭圆或双曲线之一类比(Ⅱ)写出相应的命题并
证明其真假.(只选择一种曲线解答即可,若两种都选,则以第一选择为评分依据)
已知平面内两定点 ,动点
,动点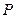 满足条件:
满足条件: ,设点
,设点 的轨迹是曲线
的轨迹是曲线 为坐标原点。
为坐标原点。
(I)求曲线 的方程;
的方程;
(II)若直线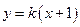 与曲线
与曲线 相交于两不同点
相交于两不同点 ,求
,求 的取值范围;
的取值范围;
(III)(文科做)设 两点分别在直线
两点分别在直线 上,若
上,若 ,记
,记 分别为
分别为 两点的横坐标,求
两点的横坐标,求 的最小值。
的最小值。
(理科做)设 两点分别在直线
两点分别在直线 上,若
上,若 ,求
,求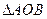 面积的最大值。
面积的最大值。
设抛物线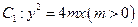 的准线与
的准线与 轴交于点
轴交于点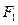 ,焦点为
,焦点为 ;椭圆
;椭圆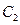 以
以 为焦点,离心率
为焦点,离心率 。
。
(I)当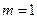 时,①求椭圆
时,①求椭圆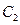 的标准方程;②若直线
的标准方程;②若直线 与抛物线交于
与抛物线交于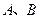 两点,且线段
两点,且线段 恰好被点
恰好被点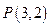 平分,设直线
平分,设直线 与椭圆
与椭圆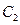 交于
交于 两点,求线段
两点,求线段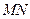 的长;
的长;
(II)(仅理科做)设抛物线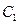 与椭圆
与椭圆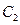 的一个交点为
的一个交点为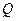 ,是否存在实数
,是否存在实数 ,使得
,使得 的边长是连续的自然数?若存在,求出这样的实数
的边长是连续的自然数?若存在,求出这样的实数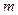 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
如图,圆 内有一点
内有一点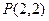 ,过点
,过点 作直线
作直线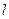 交圆于
交圆于 两点.(1)当直线
两点.(1)当直线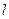 经过圆心
经过圆心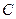 时,求直线
时,求直线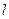 的方程;(2)当弦
的方程;(2)当弦 被点
被点 平分时,写出直线
平分时,写出直线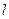 方程;(3)当直线
方程;(3)当直线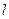 倾斜角为
倾斜角为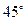 时,求
时,求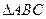 的面积.
的面积.

试题篮
()