(本小题满分14分)已知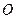 为坐标原点,点F、T、M、P分别满足
为坐标原点,点F、T、M、P分别满足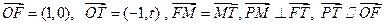 .
.
(1) 当t变化时,求点P的轨迹方程;
(2) 若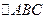 的顶点在点P的轨迹上,且点A的纵坐标
的顶点在点P的轨迹上,且点A的纵坐标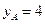 ,
,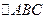 的重心恰好为点F,
的重心恰好为点F,
求直线BC的方程.
将圆 上的点的横坐标保持不变,纵坐标变为原来的
上的点的横坐标保持不变,纵坐标变为原来的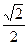 倍,得到曲线
倍,得到曲线 .设直线
.设直线 与曲线
与曲线 相交于
相交于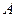 、
、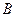 两点,且
两点,且 ,其中
,其中 是曲线
是曲线 与
与 轴正半轴的交点.
轴正半轴的交点.
(Ⅰ)求曲线 的方程;
的方程; (Ⅱ)证明:直线
(Ⅱ)证明:直线 的纵截距为定值.
的纵截距为定值.
如图,椭圆
的一个焦点是
,
为坐标原点。
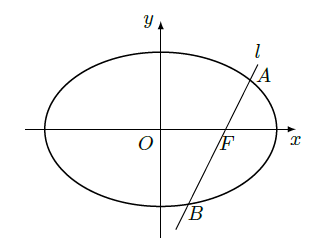
(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程;
(Ⅱ)设过点
的直线
交椭圆于
、
两点,若直线
绕点
任意转动,值有
,求
的取值范围。
如图,已知
的两条角平分线
和
相交于
,
,
在
上,且
.
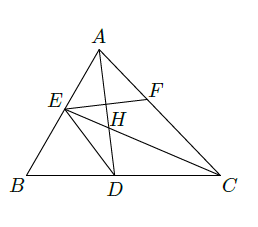
(Ⅰ)证明:
、
、
、
四点共圆;
(Ⅱ)证明:
平分
.
(本题满分16分)本题共有2个小题,第1小题满分6分,第2小题满分10分.
已知两点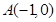 、
、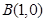 ,点
,点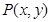 是直角坐标平面上的动点,若将点
是直角坐标平面上的动点,若将点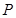 的横坐标保持不变、纵坐标扩大到
的横坐标保持不变、纵坐标扩大到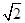 倍后得到点
倍后得到点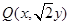 满足
满足 .
.
(1) 求动点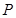 所在曲线
所在曲线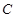 的轨迹方程;
的轨迹方程;
(2)(理科)过点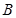 作斜率为
作斜率为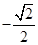 的直线
的直线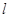 交曲线
交曲线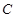 于
于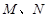 两点,且满足
两点,且满足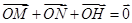 ,又点
,又点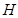 关于原点O的对称点为点
关于原点O的对称点为点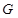 ,试问四点
,试问四点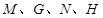 是否共圆,若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
是否共圆,若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
(文科)过点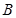 作斜率为
作斜率为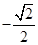 的直线
的直线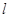 交曲线
交曲线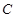 于
于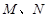 两点,且满足
两点,且满足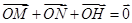 (O为坐标原点),试判断点
(O为坐标原点),试判断点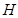 是否在曲线
是否在曲线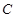 上,并说明理由.
上,并说明理由.
已知平面内两定点 ,动点
,动点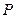 满足条件:
满足条件: ,设点
,设点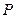 的轨迹是曲线
的轨迹是曲线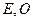 为坐标原点。
为坐标原点。
(I)求曲线 的方程;
的方程;
(II)若直线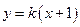 与曲线
与曲线 相交于两不同点
相交于两不同点 ,求
,求 的取值范围;
的取值范围;
(III)(文科做)设 两点分别在直线
两点分别在直线 上,若
上,若 ,记
,记 分别为
分别为 两点的横坐标,求
两点的横坐标,求 的最小值。
的最小值。
(理科做)设 两点分别在直线
两点分别在直线 上,若
上,若 ,求
,求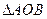 面积的最大值。
面积的最大值。
已知椭圆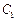 和抛物线
和抛物线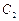 有公共焦点F(1,0),
有公共焦点F(1,0), 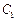 的中心和
的中心和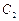 的顶点都在坐标原点,过点M(4,0)的直线
的顶点都在坐标原点,过点M(4,0)的直线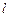 与抛物线
与抛物线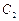 分别相交于A,B两点.
分别相交于A,B两点.
(Ⅰ)写出抛物线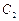 的标准方程;
的标准方程;
(Ⅱ)若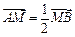 ,求直线
,求直线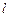 的方程;
的方程;
(Ⅲ)若坐标原点 关于直线
关于直线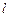 的对称点
的对称点 在抛物线
在抛物线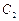 上,直线
上,直线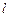 与椭圆
与椭圆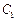 有公共点,求椭圆
有公共点,求椭圆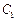 的长轴长的最小值.
的长轴长的最小值.
设抛物线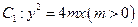 的准线与
的准线与 轴交于点
轴交于点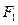 ,焦点为
,焦点为 ;椭圆
;椭圆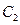 以
以 为焦点,离心率
为焦点,离心率 。
。
(I)当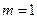 时,①求椭圆
时,①求椭圆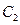 的标准方程;②若直线
的标准方程;②若直线 与抛物线交于
与抛物线交于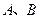 两点,且线段
两点,且线段 恰好被点
恰好被点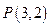 平分,设直线
平分,设直线 与椭圆
与椭圆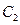 交于
交于 两点,求线段
两点,求线段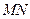 的长;
的长;
(II)(仅理科做)设抛物线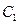 与椭圆
与椭圆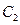 的一个交点为
的一个交点为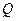 ,是否存在实数
,是否存在实数 ,使得
,使得 的边长是连续的自然数?若存在,求出这样的实数
的边长是连续的自然数?若存在,求出这样的实数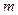 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
试题篮
()