(本题满分15分)圆C过点A(2,0)及点B( ,
,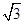 ),且与直线l:y=
),且与直线l:y= 相切
相切
(1)求圆C的方程;
(2)过点P(2,1)作圆C的切线,切点为M,N,求|MN|;
(3)点Q为圆C上第二象限内一点,且∠BOQ= ,求Q点横坐标.
,求Q点横坐标.
(本小题满分12分)已知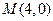 ,
,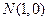 ,若动点
,若动点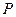 满足
满足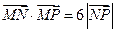 ,
,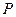 点的轨迹为曲线
点的轨迹为曲线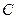 .
.
(Ⅰ)求曲线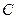 的方程;
的方程;
(Ⅱ)试确定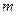 的取值范围,使得对于直线
的取值范围,使得对于直线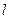 :
: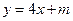 ,曲线
,曲线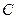 上总有不同的两点关于直线
上总有不同的两点关于直线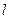 对称.
对称.
已知曲线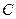 的极坐标方程为
的极坐标方程为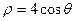 ,直线
,直线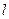 的参数方程是:
的参数方程是: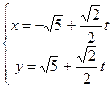
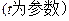 .
.
(Ⅰ)求曲线 的直角坐标方程,直线
的直角坐标方程,直线 的普通方程;
的普通方程;
(Ⅱ)将曲线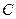 横坐标缩短为原来的
横坐标缩短为原来的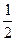 ,再向左平移1个单位,得到曲线曲线
,再向左平移1个单位,得到曲线曲线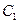 ,求曲线
,求曲线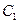 上的点到直线
上的点到直线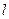 距离的最小值.
距离的最小值.
( 10分)已知双曲线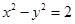 的左、右焦点分别为
的左、右焦点分别为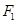 ,
, ,过点
,过点 的动直线与双曲线相交于
的动直线与双曲线相交于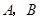 两点.
两点.
(I)若动点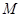 满足
满足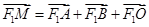 (其中
(其中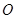 为坐标原点),求点
为坐标原点),求点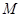 的轨迹方程;
的轨迹方程;
(II)在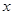 轴上是否存在定点
轴上是否存在定点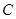 ,使
,使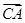 ·
·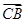 为常数?若存在,求出点
为常数?若存在,求出点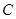 的坐标;
的坐标;
若不存在,请说明理由.
(本小题满分12分)双曲线 的离心率为
的离心率为 ,右准线为
,右准线为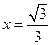 。
。
(Ⅰ)求双曲线C的方程;
(Ⅱ)已知直线 与双曲线C交于不同的两点A,B,且线段AB的中点在圆
与双曲线C交于不同的两点A,B,且线段AB的中点在圆 上,求m的值.
上,求m的值.
已知 是两条不同的直线,
是两条不同的直线, 是一个平面,有下列四个命题:
是一个平面,有下列四个命题:
① 若 ,则
,则 ; ② 若
; ② 若 ,则
,则 ;
;
③ 若 ,则
,则 ;④ 若
;④ 若 ,则
,则 .
.
其中真命题的序号有 .(请将真命题的序号都填上)
(本小题满分13分)双曲线的中心是原点O,它的虚轴长为 ,相应于焦点F(c,0)(c>0)的准线
,相应于焦点F(c,0)(c>0)的准线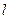 与x轴交于点A,且|OF|=3|OA|,过点F的直线与双曲线交于P、Q两点.
与x轴交于点A,且|OF|=3|OA|,过点F的直线与双曲线交于P、Q两点.
(1)求双曲线的方程;
(2)若 =0,求直线PQ的方程.
=0,求直线PQ的方程.
已知椭圆E: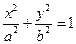 (
(


 0)过点(0,
0)过点(0,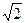 ),其左焦点
),其左焦点 与点P(1,
与点P(1,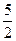 )的连线与圆
)的连线与圆 相切。
相切。
(1)求椭圆E的方程;
(2)设Q为椭圆E上的一个动点,试判断以 为直径的圆与圆
为直径的圆与圆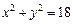 的位置关系,并证明
的位置关系,并证明
已知点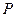 为圆周
为圆周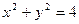 的动点,过
的动点,过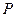 点作
点作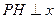 轴,垂足为
轴,垂足为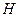 ,设线段
,设线段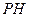 的中点为
的中点为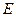 ,记点
,记点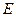 的轨迹方程为
的轨迹方程为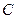 ,点
,点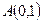
(1)求动点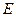 的轨迹方程
的轨迹方程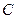 ;
;
(2)若斜率为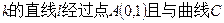 的另一个交点为
的另一个交点为 ,求
,求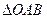 面积的最大值及此时直线
面积的最大值及此时直线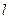 的方程;
的方程;
(3)是否存在方向向量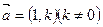 的直线
的直线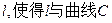 交与两个不同的点
交与两个不同的点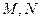 ,且有
,且有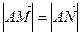 ?若存在,求出
?若存在,求出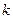 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
试题篮
()