在极坐标系中,已知圆C的圆心坐标为(3,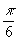 ),半径为1,点Q在圆C上运动,O为极点。
),半径为1,点Q在圆C上运动,O为极点。
(1)求圆C的极坐标方程;
(2)若点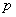 在直线OQ上运动,且满足
在直线OQ上运动,且满足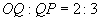 ,求动点P的轨迹方程。
,求动点P的轨迹方程。
抛物线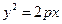 的准线的方程为
的准线的方程为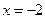 ,该抛物线上的每个点到准线
,该抛物线上的每个点到准线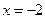 的距离都与到定点
的距离都与到定点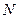 的距离相等,圆
的距离相等,圆 是以
是以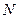 为圆心,同时与直线
为圆心,同时与直线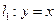 和
和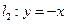 相切的圆,
相切的圆,
(Ⅰ)求定点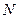 的坐标;
的坐标;
(Ⅱ)是否存在一条直线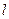 同时满足下列条件:
同时满足下列条件:
①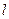 分别与直线
分别与直线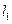 和
和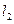 交于
交于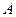 、
、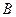 两点,且
两点,且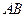 中点为
中点为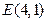 ;
;
②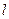 被圆
被圆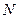 截得的弦长为2.
截得的弦长为2.
将圆 上的点的横坐标保持不变,纵坐标变为原来的
上的点的横坐标保持不变,纵坐标变为原来的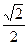 倍,得到曲线
倍,得到曲线 .设直线
.设直线 与曲线
与曲线 相交于
相交于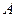 、
、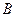 两点,且
两点,且 ,其中
,其中 是曲线
是曲线 与
与 轴正半轴的交点.
轴正半轴的交点.
(Ⅰ)求曲线 的方程;
的方程; (Ⅱ)证明:直线
(Ⅱ)证明:直线 的纵截距为定值.
的纵截距为定值.
已知圆C: 内有一点P(2,2),过点P作直线l交圆C于A、B两点.
内有一点P(2,2),过点P作直线l交圆C于A、B两点.
(1)当l经过圆心C时,求直线l的方程;
(2)当弦AB被点P平分时,写出直线l的方程;
(3)当直线l的倾斜角为45º时,求弦AB的长.
已知 过定点
过定点 ,圆心
,圆心 在抛物线
在抛物线 :
: 上运动,
上运动, 为圆
为圆 在
在 轴上所截得的弦.
轴上所截得的弦.
⑴当 点运动时,
点运动时, 是否有变化?并证明你的结论;
是否有变化?并证明你的结论;
⑵当 是
是 与
与 的等差中项时,
的等差中项时,
试判断抛物线 的准线与圆
的准线与圆 的位置关系,
的位置关系,
并说明理由。
试题篮
()