高中数学随机思想的发展试题

(本小题满分13分)
重庆电视台的一个智力游戏节目中，有一道将中国四大名著A、B、C、D与它们的作者
连线的题目，每本名著只能与一名作者连线，每名作者也只能与一本名著连线．每连对
一个得3分，连错得分，一名观众随意连线，将他的得分记作ξ．
（Ⅰ）求该观众得分ξ为正数的概率；
（Ⅱ）求ξ的分布列及数学期望．

（本小题满分12分）口袋中装有除颜色，编号不同外，其余完全相同的2个红球，4个黑球，现从中同时取出3个球．
（1）求恰有两个黑球的概率； 
（2）记取出红球的个数为随机变量，求的分布列和数学期望．

（本小题满分12分）
某地区对12岁儿童瞬时记忆能力进行调查．瞬时记忆能力包括听觉记忆能力与视觉记忆能力.某班学生共有40人，下表为该班学生瞬时记忆能力的调查结果．例如表中听觉记忆能力为中等，且视觉记忆能力偏高的学生为3人．

视觉	视觉记忆能力
偏低	中等	偏高	超常
听觉 记忆 能力	偏低	0	7	5	1
中等	1	8	3
偏高	2		0	1
超常	0	2	1	1

由于部分数据丢失，只知道从这40位学生中随机抽取一个，视觉记忆能力恰为中等，且听觉记忆能力为中等或中等以上的概率为．
（1）试确定、的值；
（2）从40人中任意抽取3人，求其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率；
（3）从40人中任意抽取3人，设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为，求随机变量的数学期望．

（本小题满分13分）国家环境标准制定的空气质量指数（简称AQI）与空气质量等级对应关系如下表：

空气质量等级	优	良	轻度污染	中度污染	重度污染	严重污染
AQI值范围	[0,50）	[50，100）	[100,150）	[150,200）	[200,300）	300及以上

 
下表是由天气网获得的全国东西部各6个城市2015年3月某时刻实时监测到的数据：

西部城市	AQI数值	东部城市	AQI数值
西安	108	北京	104
西宁	92	金门	42
克拉玛依	37	上海	x
鄂尔多斯	56	苏州	114
巴彦淖尔	61	天津	105
库尔勒	456	石家庄	93
AQI平均值：135	AQI平均值：90

 
（Ⅰ）求x的值，并根据上表中的统计数据，判断东、西部城市AQI数值的方差的大小关系（只需写出结果）；
（Ⅱ）环保部门从空气质量“优”和“轻度污染”的两类城市随机选取个城市组织专家进行调研，记选到空气质量“轻度污染”的城市个数为，求的分布列和数学期望．

在医学生物学试验中，经常以果蝇作为试验对象，一个关有6只果蝇的笼子里，不慎混入了两只苍蝇（此时笼内共有8只蝇子：6只果蝇和2只苍蝇），只好把笼子打开一个小孔，让蝇子一只一只地往外飞，直到两只苍蝇都飞出，再关闭小孔.以 $\xi$表示笼内还剩下的果蝇的只数.
（Ⅰ）写出 $\xi$的分布列（不要求写出计算过程）；
（Ⅱ）求数学期望 $E\xi$；
（Ⅲ）求概率 $P(\xi \ge E\xi )$.

一个商场经销某种商品，根据以往资料统计，每位顾客采用的分期付款次数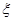的分布列为：

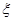	1	2	3	4	5
P	0.4	0.2	0.2	0.1	0.1

 
商场经销一件该商品，采用1期付款，其利润为200元；采用2期或3期付款，其利润为250元；采用4期或5期付款，其利润为300元.表示经销一件该商品的利润.
（1）求购买该商品的3位顾客中，恰有2位采用1期付款的概率；
（2）求的分布列及期望．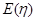

(本小题满分12分) 甲、乙、丙三人按下面的规则进行乒乓球比赛: 第一局由甲、乙参加而丙轮空，以后每一局由前一局的获胜者与轮空者进行比赛，而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为，且各局胜负相互独立.
求：（I）打满3局比赛还未停止的概率；
（II）比赛停止时已打局数的分别列与期望E.

（本小题满分12分）
右图为某校语言类专业N名毕业生的综合测评成绩（百分制）分布直方图，已知80~90分数段的学员数为21人

（I）求该专业毕业总人数N和90~95分数段内的人数；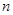
（II）现欲将90~95分数段内的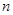名毕业生分配往甲、乙、丙三所学校，若向学校甲分配两名毕业生，且其中至少有一名男生的概率为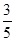，求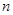名毕业生中男女各几人（男女人数均至少两人）？
（III）在（II）的结论下，设随机变量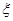表示n名毕业生中分配往乙学校的三名学生中男生的人数，求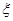的分布列和数学期望.

某公司从大学招收毕业生，经过综合测试，录用了14名男生和6名女生，这20名毕业生的测试成绩如茎叶图所示（单位：分）．公司规定：成绩在180分以上者到甲部门工作，180分以下者到乙部门工作，另外只有成绩高于180分的男生才能担任助理工作．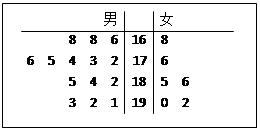

（1）如果用分层抽样的方法从甲部门人选和乙部门人选中选取8人，再从这8人中选3人，那么至少有一人是甲部门人选的概率是多少？
（2）若从所有甲部门人选中随机选3人，用X表示所选人员中能担任助理工作的人数，写出X的分布列，并求出X的数学期望．

为了解今年某校高三毕业班准备报考飞行员学生的体重情况，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1:2:3，其中第2小组的频数为12．

（Ⅰ）求该校报考飞行员的总人数；
（Ⅱ）以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的同学中（人数很多）任选三人，设X表示体重超过60公斤的学生人数，求X的分布列和数学期望．

现对某市工薪阶层关于“楼市限购令”的态度进行调查，随机抽调了人，他们月收入的频数分布及对“楼市限购令”赞成人数如下表．

月收入（单位百元）
频数
赞成人数

（I）由以上统计数据填下面列联表并问是否有%的把握认为“月收入以为分界点”对“楼市限购令”的态度有差异；

	月收入低于百元的人数	月收入低于百元的人数	合计
赞成
不赞成
合计

（II）若对月收入在，的被调查人中各随机选取两人进行追踪调查，记选中的人中不赞成“楼市限购令”人数为，求随机变量的分布列及数学期望．
参考数据：

（本小题满分12分）已知2件次品和3件正品混放在一起，现需要通过检测将其区分，
每次随机检测一件产品，检测后不放回，直到检测出2件次品或者检测出3件正品时检测
结束．
（1）求第一次检测出的是次品且第二次检测出的是正品的概率；
（2）己知每检测一件产品需要费用1 00元，设X表示直到检测出2件次品或者检测
出3件正品时所需要的检测费用（单位：元），求X的分布列和均值（数学期望）．

（满分12分）甲、乙、丙三人独立破译同一份密码，已知甲、乙、丙各自破译出密码的概率分别为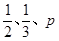。且他们是否破译出密码互不影响。若三人中只有甲破译出密码的概率为。
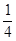（Ⅰ）求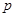的值；
（Ⅱ）设甲、乙、丙三人中破译出密码的人数为X，求X得分布列和数学期望EX。

（本小题满分12分）某城市有东西南北四个进入城区主干道的入口，在早高峰时间段，时常发生交通拥堵现象，交警部门统计11月份30天内的拥堵天数，东西南北四个主干道入口的拥堵天数分别是18天，15天，9天，15天．假设每个入口发生拥堵现象互相独立，视频率为概率．
（1）求该城市一天中早高峰时间段恰有三个入口发生拥堵的概率；
（2）设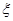表示一天中早高峰时间段发生拥堵的主干道入口个数，求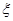的分布列和数学期望．

某公司生产产品A，产品质量按测试指标分为：指标大于或等于90为一等品，大于或等于小于为二等品，小于为三等品，生产一件一等品可盈利50元，生产一件二等品可盈利元，生产一件三等品亏损10元．现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测，检测结果统计如下：

测试指标
甲	3	7	20	40	20	10
乙	5	15	35	35	7	3

 
现将根据上表统计得到甲、乙两人生产产品A为一等品、二等品、三等品的频率分别估计为他们生产产品A为一等品、二等品、三等品的概率．
（1）计算新工人乙生产三件产品A，给工厂带来盈利大于或等于100元的概率；
（2）记甲乙分别生产一件产品A给工厂带来的盈利和记为X，求随机变量X的概率分布和数学期望．