（本小题满分12分）根据公安部最新修订的《机动车驾驶证申领和使用规定》：每位驾驶证申领者必须通过《科目一》（理论科目）、《综合科》（驾驶技能加科目一的部分理论）的考试．已知李先生已通过《科目一》的考试，且《科目一》的成绩不受《综合科》的影响，《综合科》三年内有5次预约考试的机会，一旦某次考试通过，便可领取驾驶证，不再参加以后的考试，否则就一直考到第5次为止．设李先生《综合科》每次参加考试通过的概率依次为0．5，0．6，0．7，0．8，0．9．
（1）求在三年内李先生参加驾驶证考试次数
的分布列和数学期望；
（2）求李先生在三年内领到驾驶证的概率．
（本小题满分13分）甲、乙两支篮球队赛季总决赛采用7场4胜制，每场必须分出胜负，场与场之间互不影响，只要有一队获胜4场就结束比赛．现已比赛了4场，且甲篮球队胜3场．已知甲球队第5，6场获胜的概率均为
，但由于体力原因，第7场获胜的概率为
．
（1）求甲队分别以
，
获胜的概率；
（2）设X表示决出冠军时比赛的场数，求X的分布列及数学期望．
【原创】（本小题满分14分）据报道，中国经济虽然有所下滑，但仍处于可控状态，从中央到地方对中国经济都抱有信心，因此股市的上证指数从去年的低点1974.38，涨到今天3286.07，为了了解股民的收益状况，某证券公司随机抽取
位股民目前的战绩情况，数据显示这些股民的收益目前在所有股民中所占的百分数据，用茎叶图形式表示如下：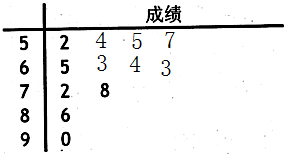
根据百分数据，成绩不低于80的为市场赢家．
（1）将频率视为概率，根据样本估计总体的思想，在股民中任选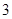
人，求至少有
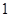人为“市场赢家”的概率；
（2）从抽取的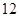人中随机选取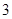人，记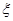
表示“市场赢家”人数，求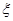的分布列及期望．
某学校研究性学习小组对该校高三学生视力情况进行调查，在高三的全体1000名学生中随机抽取了100名学生的体检表，并得到如图的频率分布直方图．
（1）若直方图中后四组的频数成等差数列，试估计全年级视力在5．0以下的人数；
（2）学习小组成员发现，学习成绩突出的学生，近视的比较多，为了研究学生的视力与学习成绩是否有
关系，对年级名次在
名和
名的学生进行了调查，得到右表中数据，根据表中的数据，
能否在犯错的概率不超过0．05的前提下认为视力与学习成绩有关系?
（3）在（2）中调查的100名学生中，按照分层抽样在不近视的学生中抽取了9人，进一步调查他们良好
的护眼习惯，并且在这9人中任取3人，记名次在的学生人数为
，求的分布列和数学期望．
附：
如图是在竖直平面内的一个“通道游戏”．图中竖直线段和斜线段都表示通道，并且在交点处相遇，若竖直线段有一条的为第一层，有二条的为第二层， ，依次类推．现有一颗小弹子从第一层的通道里向下运动，若在通道的分叉处，小弹子以相同的概率落入每个通道．记小弹子落入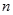第
层第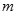
个竖直通道（从左至右）的概率为
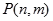，某研究性学习小组经探究发现小弹子落入第
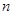层的第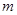
个通道的次数服从二项分布，请你解决下列问题．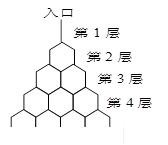
（Ⅰ）试求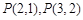
及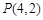
的值，并猜想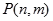的表达式；（不必证明）
（Ⅱ）设小弹子落入第6层第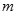个竖直通道得到分数为
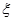，其中
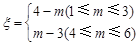，试求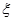的分布列及数学期望．
（本小题满分12分）口袋中装有除颜色，编号不同外，其余完全相同的2个红球，4个黑球，现从中同时取出3个球．
（1）求恰有两个黑球的概率；
（2）记取出红球的个数为随机变量
，求的分布列和数学期望
．
（本小题满分13分）国家环境标准制定的空气质量指数（简称AQI）与空气质量等级对应关系如下表：
| 空气质量等级 |
优 |
良 |
轻度污染 |
中度污染 |
重度污染 |
严重污染 |
| AQI值范围 |
[0,50） |
[50，100） |
[100,150） |
[150,200） |
[200,300） |
300及以上 |
下表是由天气网获得的全国东西部各6个城市2015年3月某时刻实时监测到的数据：
| 西部城市 |
AQI数值 |
东部城市 |
AQI数值 |
| 西安 |
108 |
北京 |
104 |
| 西宁 |
92 |
金门 |
42 |
| 克拉玛依 |
37 |
上海 |
x |
| 鄂尔多斯 |
56 |
苏州 |
114 |
| 巴彦淖尔 |
61 |
天津 |
105 |
| 库尔勒 |
456 |
石家庄 |
93 |
| AQI平均值：135 |
AQI平均值：90 |
（Ⅰ）求x的值，并根据上表中的统计数据，判断东、西部城市AQI数值的方差的大小关系（只需写出结果）；
（Ⅱ）环保部门从空气质量“优”和“轻度污染”的两类城市随机选取
个城市组织专家进行调研，记选到空气质量“轻度污染”的城市个数为
，求的分布列和数学期望．
一个商场经销某种商品，根据以往资料统计，每位顾客采用的分期付款次数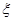
的分布列为：
|
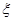1 |
2 |
3 |
4 |
5 |
| P |
0.4 |
0.2 |
0.2 |
0.1 |
0.1 |
商场经销一件该商品，采用1期付款，其利润为200元；采用2期或3期付款，其利润为250元；采用4期或5期付款，其利润为300元.
表示经销一件该商品的利润.
（1）求购买该商品的3位顾客中，恰有2位采用1期付款的概率；
（2）求的分布列及期望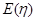
．
（本小题满分12分）
右图为某校语言类专业N名毕业生的综合测评成绩（百分制）分布直方图，已知80~90分数段的学员数为21人
（I）求该专业毕业总人数N和90~95分数段内的人数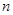
；
（II）现欲将90~95分数段内的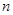名毕业生分配往甲、乙、丙三所学校，若向学校甲分配两名毕业生，且其中至少有一名男生的概率为
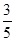，求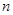名毕业生中男女各几人（男女人数均至少两人）？
（III）在（II）的结论下，设随机变量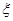
表示n名毕业生中分配往乙学校的三名学生中男生的人数，求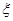的分布列和数学期望.
某公司从大学招收毕业生，经过综合测试，录用了14名男生和6名女生，这20名毕业生的测试成绩如茎叶图所示（单位：分）．公司规定：成绩在180分以上者到甲部门工作，180分以下者到乙部门工作，另外只有成绩高于180分的男生才能担任助理工作．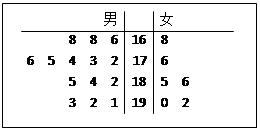
（1）如果用分层抽样的方法从甲部门人选和乙部门人选中选取8人，再从这8人中选3人，那么至少有一人是甲部门人选的概率是多少？
（2）若从所有甲部门人选中随机选3人，用X表示所选人员中能担任助理工作的人数，写出X的分布列，并求出X的数学期望．
为了解今年某校高三毕业班准备报考飞行员学生的体重情况，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1:2:3，其中第2小组的频数为12．
（Ⅰ）求该校报考飞行员的总人数；
（Ⅱ）以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的同学中（人数很多）任选三人，设X表示体重超过60公斤的学生人数，求X的分布列和数学期望．
现对某市工薪阶层关于“楼市限购令”的态度进行调查，随机抽调了
人，他们月收入的频数分布及对“楼市限购令”赞成人数如下表．
| 月收入（单位百元） |
 |
 |
 |
 |
 |
 |
| 频数 |
 |
 |
 |
|
|
|
| 赞成人数 |
 |
 |
 |
|
 |
 |
（I）由以上统计数据填下面
列联表并问是否有
%的把握认为“月收入以
为分界点”对“楼市限购令”的态度有差异；
| |
月收入低于 百元的人数 |
月收入低于百元的人数 |
合计 |
| 赞成 |
 |
 |
|
| 不赞成 |
 |
 |
|
| 合计 |
|
|
|
（II）若对月收入在，的被调查人中各随机选取两人进行追踪调查，记选中的人中不赞成“楼市限购令”人数为
，求随机变量的分布列及数学期望．
参考数据：
 |
 |
 |
 |
 |
 |
 |
 |
（本小题满分12分）已知2件次品和3件正品混放在一起，现需要通过检测将其区分，
每次随机检测一件产品，检测后不放回，直到检测出2件次品或者检测出3件正品时检测
结束．
（1）求第一次检测出的是次品且第二次检测出的是正品的概率；
（2）己知每检测一件产品需要费用1 00元，设X表示直到检测出2件次品或者检测
出3件正品时所需要的检测费用（单位：元），求X的分布列和均值（数学期望）．
（满分12分）甲、乙、丙三人独立破译同一份密码，已知甲、乙、丙各自破译出密码的概率分别为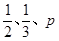
。且他们是否破译出密码互不影响。若三人中只有甲破译出密码的概率为
。
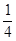（Ⅰ）求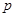
的值；
（Ⅱ）设甲、乙、丙三人中破译出密码的人数为X，求X得分布列和数学期望EX。
（本小题满分12分）某城市有东西南北四个进入城区主干道的入口，在早高峰时间段，时常发生交通拥堵现象，交警部门统计11月份30天内的拥堵天数，东西南北四个主干道入口的拥堵天数分别是18天，15天，9天，15天．假设每个入口发生拥堵现象互相独立，视频率为概率．
（1）求该城市一天中早高峰时间段恰有三个入口发生拥堵的概率；
（2）设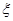
表示一天中早高峰时间段发生拥堵的主干道入口个数，求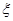的分布列和数学期望．
试题篮
()
粤公网安备 44130202000953号
