（本小题满分12分）西安市某中学在每年的11月份都会举行“文化艺术节”，开幕式当天组织举行大型的文艺表演，同时邀请36名不同社团的社长进行才艺展示．其中有
的社长是高中学生，
的社长是初中学生，高中社长中有
是高一学生，初中社长中有
是初二学生．
（Ⅰ）若校园电视台记者随机采访3位社长，求恰有1人是高一学生且至少有1人是初中学生的概率；
（Ⅱ）若校园电视台记者随机采访3位初中学生社长，设初二学生人数为
，求的分布列及数学期望
．
一个袋子装有大小形状完全相同的9个球，其中5个红球编号分别为1,2,3,4,5,4个白球编号分别为1,2,3,4，从袋中任意取出3个球．
（Ⅰ）求取出的3个球编号都不相同的概率；
（Ⅱ）记
为取出的3个球中编号的最小值，求的分布列与数学期望．
（本小题满分12分）口袋中装有除颜色，编号不同外，其余完全相同的2个红球，4个黑球．现从中同时取出3个球．
（Ⅰ）求恰有一个黑球的概率；
（Ⅱ）记取出红球的个数为随机变量
，求的分布列和数学期望
．
（本小题满分12分）下图是某市今年1月份前30天空气质量指数（AQI）的趋势图.
（1）根据该图数据在答题卷中完成频率分布表，并在图中作出这些数据的频率分布直方图；
（图中纵坐标1/300即
，以此类推）
（2）当空气质量指数（AQI）小于100时，表示空气质量优良．某人随机选择当月1日至10日中的某一
天到达该市，并停留2天，设
是此人停留期间空气质量优良的天数，求的数学期望．
射击测试有两种方案，方案1：先在甲靶射击一次，以后都在乙靶射击；方案2：始终在乙靶射击，某射手命中甲靶的概率为
，命中一次得3分；命中乙靶的概率为
，命中一次得2分，若没有命中则得0分，用随机变量
表示该射手一次测试累计得分，如果的值不低于3分就认为通过测试，立即停止射击；否则继续射击，但一次测试最多打靶3次，每次射击的结果相互独立。
（1）如果该射手选择方案1，求其测试结束后所得分的分布列和数学期望E；
（2）该射手选择哪种方案通过测试的可能性大？请说明理由。
【改编】（本小题满分12分）贵广高速铁路自贵阳北站起，经黔南州、黔东南、广西桂林、贺州、广东肇庆、佛山终至广州南站．其中广东省内有怀集站、广宁站、肇庆东站、三水南站、佛山西站、广州南站共6个站．记者对广东省内的6个车站随机抽取3个进行车站服务满意度调查．
（1）求抽取的车站中不含佛山市内车站（包括三水南站和佛山西站）的概率；
（2）设抽取的车站中含有肇庆市内车站（包括怀集站、广宁站、肇庆东站）个数为X，求X的分布列及其均值（即数学期望）．
（本小题满分12分）下图为某校语言类专业N名毕业生的综合测评成绩（百分制）分布直方图，已知80~90分数段的学员数为21人
（Ⅰ）求该专业毕业总人数N和90~95分数段内的人数
；
（Ⅱ）现欲将90~95分数段内的名毕业生分配往甲、乙、丙三所学校，若向学校甲分配两名毕业生，且其中至少有一名男生的概率为
，求名毕业生中男女各几人（男女人数均至少两人）？
（Ⅲ）在（Ⅱ）的结论下，设随机变量
表示n名毕业生中分配往乙学校的三名学生中男生的人数，求的分布列和数学期望．
（本小题12分）据报道，全国很多省市将英语考试作为高考改革的重点，一时间“英语考试该如何改革”引起广泛关注，为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法，某媒体在该地区选择了3600人进行调查，就“是否取消英语听力”问题进行了问卷调查统计，结果如下表：
| 态度 调查人群 |
应该取消 |
应该保留 |
无所谓 |
| 在校学生 |
2100人 |
120人 |
 人 |
| 社会人士 |
600人 |
 人 |
 人 |
（1）已知在全体样本中随机抽取
人，抽到持“应该保留”态度的人的概率为
，现用分层抽样的方法在所有参与调查的人中抽取
人进行问卷访谈，问应在持“无所谓”态度的人中抽取多少人？
（2）在持“应该保留”态度的人中，用分层抽样的方法抽取
人，再平均分成两组进行深入交流，求第一组中在校学生人数
的分布列和数学期望．
（本小题满分12分）甲乙两人进行围棋比赛，约定先连胜两局者直接赢得比赛，若赛完
局仍未出现连胜，则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为
，乙获胜的概率为
，各局比赛结果相互独立.
（1）求甲在
局以内（含局）赢得比赛的概率；
（2）记
为比赛决出胜负时的总局数，求的分布列和期望.
为选拔选手参加“中国汉字听写大会”，某中学举行了一次“汉字听写大赛”活动．为了了解本次竞赛学生的成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100分）作为样本（样本容量为
）进行统计．按照
，
，
，
，
的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出了得分在，的数据）．
（1）求样本容量和频率分布直方图中的
、
的值；
（2）在选取的样本中，从竞赛成绩在80分以上（含80分）的学生中随机抽取3名学生参加“中国汉字听写大会”，设随机变量
表示所抽取的3名学生中得分在内的学生人数，求随机变量的分布列及数学期望．
（本小题满分12分）学校为测评班级学生对任课教师的满意度，采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名，以下茎叶图记录了他们对某教师的满意度分数（以十位数字为茎，个位数字为叶）：规定若满意度不低于98分，测评价该教师为“优秀”.
（1）求从这10人中随机选取3人，至多有1人评价该教师是“优秀”的概率；
（2）以这10人的样本数据来估计整个班级的总体数据，若从该班任选3人，记
表示抽到评价该教师为“优秀”的人数，求的分布列及数学期望.
（本小题满分13分）某工厂生产A，B两种型号的玩具，其质量按测试指标划分为：指标大于或等于82为正品，小于82为次品．现随机抽取这两种玩具各100件进行检测，检测结果统计如下：
| 测试指标 |
[70,76） |
[76,82） |
[82,88） |
[88,94） |
[94,100） |
| 玩具A |
8 |
12 |
40 |
32 |
8 |
| 玩具B |
7 |
18 |
40 |
29 |
6 |
（Ⅰ）试分别估计玩具A、玩具B为正品的概率；
（Ⅱ）生产一件玩具A，若是正品可盈利40元，若是次品则亏损5元；生产一件玩具B，若是正品可盈利50元，若是次品则亏损10元．在（I）的前提下，
（i）记X为生产1件玩具A和1件玩具B所得的总利润，求随机变量X的分布列和数学期望；
（ii）求生产5件玩具B所获得的利润不少于140元的概率．
（本小题满分12分）根据我国发布了新修订的《环境空气质量标准》指出空气质量指数在
为优秀，人类可正常活动．某市环保局对该市2014年进行为期一年的空气质量监测，得到每天的空气质量指数，从中随机抽取50个作为样本进行分析报告，样本数据分组区间为
，
， 
， 
，由此得到样本的空气质量指数频率分布直方图．
（Ⅰ）若空气质量指数大于或等于15且小于35认为是良好的，求该市在这次监测中空气质量
为良好的天数，并根据频率分布直方图估计这一年度的空气质量指数的平均值；
（Ⅱ）如果空气质量指数不超过15，就认定空气质量为“优”，则从这一年的监测数据中随机
抽取3天的数值，其中达到“优”的天数为
，求的分布列和数学期望．
（本小题12分）据报道，全国很多省市将英语考试作为高考改革的重点，一时间“英语考试该如何改革”引起广泛关注，为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法，某媒体在该地区选择了3600人进行调查，就“是否取消英语听力”问题进行了问卷调查统计，结果如下表：
| 态度 调查人群 |
应该取消 |
应该保留 |
无所谓 |
| 在校学生 |
2100人 |
120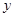人 |
 人 |
| 社会人士 |
600人 |
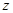 人 |
 人 |
（1）已知在全体样本中随机抽取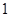
人，抽到持“应该保留”态度的人的概率为
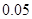，现用分层抽样的方法在所有参与调查的人中抽取
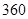人进行问卷访谈，问应在持“无所谓”态度的人中抽取多少人？
（2）在持“应该保留”态度的人中，用分层抽样的方法抽取
人，再平均分成两组进行深入交流，求第一组中在校学生人数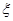
的分布列和数学期望.
（本小题满分12分）根据某电子商务平台的调查统计显示，参与调查的1000位上网购物者的年龄情况如下图显示．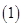
已知
、
、
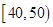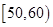三个年龄段的上网购物者人数成等差数列，求
，
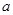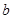的值；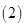
该电子商务平台将年龄在
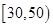之间的人群定义为高消费人群，其他的年龄段定义为潜在消费人群，为了鼓励潜在消费人群的消费，该平台决定发放代金券，高消费人群每人发放50元的代金券，潜在消费人群每人发放100元的代金券，现采用分层抽样的方式从参与调查的1000位上网购物者中抽取10人，并在这10人中随机抽取3人进行回访，求此三人获得代金券总和
的分布列与数学期望．
试题篮
()
粤公网安备 44130202000953号
