（本小题满分12分）某高中数学竞赛培训在某学段共开设有初等代数、平面几何、初等数论和微积分初步共四门课程，要求初等数论、平面几何都要合格，且初等代数和微积分初步至少有一门合格，则能取得参加数学竞赛复赛的资格．现有甲、乙、丙三位同学报名参加数学竞赛培训，每一位同学对这四门课程考试是否合格相互独立，其合格的概率均相同（见下表），且每一门课程是否合格相互独立．
（Ⅰ）求甲同学取得参加数学竞赛复赛的资格的概率；
（Ⅱ）记
表示三位同学中取得参加数学竞赛复赛的资格的人数，求的分布列及期望
．
（本小题满分12分）如图所示，某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损，其中，频率分布直方图的分组区间分别为[50，60），[60，70），[70，80），[80，90），[90，100]，据此解答如下问题．
（1）求全班人数及分数在[80，100]之间的频率；
（2）现从分数在[80，100]之间的试卷中任取
份分析学生失分情况，设抽取的试卷分数在[90，100]的份数为 X ，求 X 的分布列和数学望期．
（本小题满分13分）甲、乙、丙三人参加某次招聘会，若甲应聘成功的概率为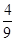
，乙、丙应聘成功的概率均为
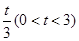，且三人是否应聘成功是相互独立的．
（Ⅰ）若甲、乙、丙都应聘成功的概率是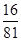
，求
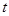的值；
（Ⅱ）在（Ⅰ）的条件下，设
表示甲、乙两人中被聘用的人数，求的数学期望．
（本小题满分12分）某校举行中学生“珍爱地球·保护家园”的环保知识比赛,比赛分为初赛和复赛两部分，初赛采用选手从备选题中选一题答一题的方式进行；每位选手最多有5次答题机会，选手累计答对3题或答错3题即终止比赛，答对3题者直接进入复赛，答错3题者则被淘汰．已知选手甲答对每个题的概率均为
，且相互间没有影响．
（Ⅰ）求选手甲进入复赛的概率；
（Ⅱ）设选手甲在初赛中答题的个数为，试求的分布列和数学期望．
（本小题满分12分）4月23人是“世界读书日”，某中学在此期间开展了一系列的读书教育活动，为了解本校学生课外阅读情况，学校随机抽取了100名学生对其课外阅读时间进行调查，下面是根据调查结果绘制的学生日均课外阅读时间（单位：分钟）的频率分布直方图，若将日均课外阅读时间不低于60分钟的学生称为“读书谜”，低于60分钟的学生称为“非读书谜”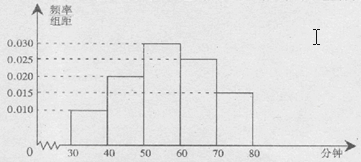
（1）根据已知条件完成下面
的列联表，并据此判断是否有99%的把握认为“读书谜”与性别有关？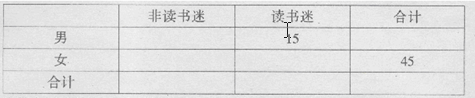
（2）将频率视为概率，现在从该校大量学生中，用随机抽样的方法每次抽取1人，共抽取3次，记被抽取的3人中的“读书谜”的人数为X，若每次抽取的结果是相互独立的，求X的分布列，期望E（X）和方差D（X）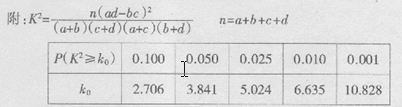
（本小题满分10分）某商店根据以往某种新产品的销售记录，绘制了日销售量的频率分布直方图，如图所示.将日销售量落入各组的频率视为概率，并假设每天的销售量相互独立.
（1）估计日销售量的众数；
（2）求在未来连续3天里，有连续2天的日销售量都不低于100个且另1天的日销售量低于50个的概率；
（3）用X表示在未来3天里日销售量不低于100个的天数，求随机变量X的分布列.
（本小题满分12分）某校对参加高校自主招生测试的学生进行模拟训练，从中抽出N名学生，其数学成绩的频率分布直方图如图所示．已知成绩在区间[90，100]内的学生人数为2人。
（1）求N的值并估计这次测试数学成绩的平均分和众数；
（2）学校从成绩在[70，100]的三组学生中用分层抽样的方法抽取12名学生进行复试，若成绩在[80，90）这一小组中被抽中的学生实力相当，且能通过复试的概率均为
，设成绩在[80，90）这一小组中被抽中的学生中能通过复试的人数为
，求的分布列和数学期望．
（本小题满分13分）
某大学志愿者协会有10名同学，成员构成如下表，其中表中部分数据不清楚，只知道从这10名同学中随机抽取一位，抽到该名同学为“数学专业”的概率为
．
| 专业 性别 |
中文 |
英语 |
数学 |
体育 |
| 男 |
 |
1 |
 |
1 |
| 女 |
1 |
1 |
1 |
1 |
现从这10名同学中随机选取3名同学参加社会公益活动（每位同学被选到的可能性相同）．
（Ⅰ）求
的值；
（Ⅱ）求选出的3名同学恰为专业互不相同的男生的概率；
（Ⅲ）设
为选出的3名同学中“女生或数学专业”的学生的人数，求随机变量的分布列及其数学期望
．
（本小题满分12分）退休年龄延迟是平均预期寿命延长和人口老龄化背景下的一种趋势．某机构
为了解某城市市民的年龄构成，从该城市市民中随机抽取年龄段在20~80岁（含20岁和80岁）之间的600
人进行调查，并按年龄层次[20，30），[30，40），[40，50），[50，60），[60，70），[70，80]绘制频率分布直方
图，如图所示．若规定年龄分布在[20，40）岁的人为“青年人”，[40，60）为“中年人”， [60，80]为“老年人”．
 |
（1）若每一组数据的平均值用该区间中点值来代替，试估算所调查的600人的平均年龄；
（2）将上述人口分布的频率视为该城市在20-80年龄段的人口分布的概率．从该城市20-80年龄段市民中
随机抽取3人，记抽到“老年人”的人数为
，求随机变量的分布列和数学期望．
(本题满分12分)
“开门大吉”是某电视台推出的游戏节目．选手面对1～8号8扇大门，依次按响门上的门铃，门铃会播放一段音乐（将一首经典流行歌曲以单音色旋律的方式演绎），选手需正确回答出这首歌的名字，方可获得该扇门对应的家庭梦想基金．在一次场外调查中，发现参赛选手多数分为两个年龄段：20～30；30～40（单位：岁），其猜对歌曲名称与否的人数如图所示．
（1）写出2×2列联表；判断是否有90%的把握认为猜对歌曲名称与否和年龄有关；说明你的理由；（下面的临界值表供参考）
 |
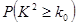0．10 |
0．05 |
0．010 |
0．005 |
 |
2．706 |
3．841 |
6．635 |
7．879 |
现计划在这次场外调查中按年龄段选取9名选手，并抽取3名幸运选手，求3名幸运选手中在20～30岁之间的人数的分布列和数学期望．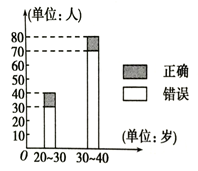
（参考公式：
其中
）
（本小题满分12分）
一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取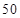
个作为样本,称出它们的重量（单位：克）,重量分组区间为
,
,
,
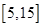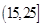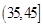,由此得到样本的重量频率分布直方图（如下图）,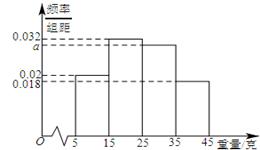
（1）求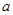
的值,并根据样本数据,试估计盒子中小球重量的众数与平均值；
（2）从盒子中随机抽取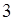
个小球,其中重量在
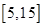内的小球个数为
,求的分布列和数学期望. (以直方图中的频率作为概率).
(本题满分10分)
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者，从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示，其中年龄分组区间是：
．
（1）求图中
的值并根据频率分布直方图估计这500名志愿者中年龄在
岁的人数；
（2）在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场的宣传活动，再从这20名中采用简单随机抽样方法选取3名志愿者担任主要负责人，记这3名志愿者中“年龄低于35岁”的人数为
，求的分布列及数学期望．
（本小题满分12分）
某校甲、乙两个班级各有5名编号为1，2，3，4，5的学生进行投篮训练，每人投10次，投中的次数统计如下表：
| 学生 |
1号 |
2号 |
3号 |
4号 |
5号 |
| 甲班 |
6 |
5 |
7 |
9 |
8 |
| 乙班 |
4 |
8 |
9 |
7 |
7 |
(Ⅰ)从统计数据看，甲乙两个班哪个班成绩更稳定（用数据说明）？
(Ⅱ) 若把上表数据作为学生投篮命中率，规定两个班级的1号和2号两名同学分别代表自己的班级参加比赛，每人投篮一次，将甲、乙两个班两名同学投中的次数之和分别记作
和
，试求和的分布列和数学期望.
甲、乙两位学生参加数学竞赛培训．现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次．记录如下：
甲：82 81 79 78 95 88 93 84
乙：92 95 80 75 83 80 90 85
（1）画出甲、乙两位学生成绩的茎叶图，指出学生乙成绩的中位数；
（2）现要从中选派一人参加数学竞赛，从平均状况和方差的角度考虑，你认为派哪位学生参加合适?请说明理由；
（3）若将频率视为概率，对学生甲在今后的三次数学竞赛成绩进行预测，记这三次成绩中高于80分的次数为
，求的分布列及数学期望
．
试题篮
()
粤公网安备 44130202000953号
，求随机变量