设x∈,集合A是奇数集,集合B是偶数集.若命题p: x∈A,2x∈B,则( )
x∈A,2x∈B,则( )
A. |
B. |
C. |
D. |
命题“所有能被2整除的数都是偶数”的否定是
A 所有不能被2整除的数都是偶数
B 所有能被2整除的数都不是偶数
C 存在一个不能被2整除的数都是偶数
D 存在一个能被2整除的数不是偶数
已知命题p:∀x∈R,sin x≤1,则( ).
| A.¬p:∃x0∈R,sin x0≥1 |
| B.¬p:∀x∈R,sin x≥1 |
| C.¬p:∃x0∈R,sin x0>1 |
| D.¬p:∀x∈R,sin x>1 |
已知命题p:∃x0∈R,使sin x0= ;命题q:∀x∈R,都有x2+x+1>0.
;命题q:∀x∈R,都有x2+x+1>0.
给出下列结论 ①命题“p∧q”是真命题; ②命题“¬p∨¬q”是假命题;
③命题“¬p∨q”是真命题; ④命题“p∨¬q”是假命题.
其中正确的是
| A.②③ |
| B.②④ |
| C.③④ |
| D.①②③ |
已知命题p:∀x1,x2∈R,(f(x2)-f(x1))(x2-x1)≥0,则¬p是( )
| A.∃x1,x2∈R,(f(x2)-f(x1))(x2-x1)≤0 |
| B.∀x1,x2∈R,(f(x2)-f(x1))(x2-x1)≤0 |
| C.∃x1,x2∈R,(f(x2)-f(x1))(x2-x1)<0 |
| D.∀x1,x2∈R,(f(x2)-f(x1))(x2-x1)<0 |
已知命题p:“∀x∈R,∃m∈R,使4x+2x·m+1=0”.若命题p为真命题,则实数m的取值范围是
| A.(-∞,-2] |
| B.[2,+∞) |
| C.(-∞,-2) |
| D.(2,+∞) |
已知命题p:∃x∈[0,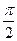 ],cos2x+cosx-m=0的否定为假命题,则实数m的取值范围是( )
],cos2x+cosx-m=0的否定为假命题,则实数m的取值范围是( )
A.[-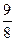 ,-1] ,-1] |
B.[-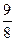 ,2] ,2] |
| C.[-1,2] |
D.[-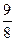 ,+∞) ,+∞) |
已知命题p:“∀x∈[1,2],x2-a≥0”;命题q:“∃x∈R,x2+2ax+2-a=0”.若命题“p且q”是真命题,则实数a的取值范围为( )
| A.a≤-2或a=1 |
| B.a≤-2或1≤a≤2 |
| C.a≥1 |
| D.-2≤a≤1 |
下列说法正确的是( )
A.命题“若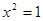 ,则 ,则 ”的否命题是“若 ”的否命题是“若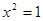 ,则 ,则 ” ” |
B.“ ”是“ ”是“ ”的必要不充分条件 ”的必要不充分条件 |
C.命题“若 ,则 ,则 ”的逆否命题是真命题 ”的逆否命题是真命题 |
D.“ ”是“ ”是“ ”的充分不必要条件 ”的充分不必要条件 |
试题篮
()