高中数学二次剩余试题

已知函数,若，且，则的取值范围为    ．

抛物线与轴的两个交点的横坐标分别为1和3，则不等式的解集是                    ．

对于任意，函数的值非负，则实数的最小值为（  ）

A．

B．-5

C．-3

D．-2

已知中心在原点，焦点在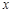轴上的椭圆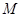的离心率为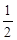，椭圆上异于长轴顶点的任意点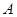与左右两焦点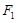、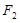构成的三角形中面积的最大值为.
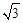（1）求椭圆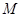的标准方程；
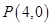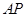（2）已知点，连接与椭圆的另一交点记为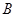，若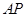与椭圆相切时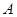、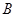不重合，连接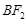与椭圆的另一交点记为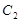，求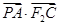的取值范围.

（本小题14分）已知函数是定义在R上的偶函数，且当≤0时，．
 
（1）求出的解析式；
（2）现已画出函数在y轴左侧的图像，如图所示，请补出完整函数的图像，并根据图像写出函数的增区间和值域。

关于的不等式的解集为，且，则（　　）

A．

B．

C．

D．

设二次函数f（x）=ax²+bx+c的图象过点（0，1）和（1，4），且对于任意的实数x，不等式f（x）≥4x恒成立．
（1）求函数f（x）的表达式；
（2）设g（x）=kx+1，若G（x）=在区间[1，2]上是增函数，求实数k的取值范围。

某公司在甲、乙两地销售一种品牌车,利润(单位：万元)分别为L₁=5.06x-0.15x²和L₂=2x,其中x为销售量(单位：辆).若该公司在这两地共销售15辆车,则能获得的最大利润为(　　)

A．45.606万元	B．45.6万元
C．45.56万元	D．45.51万元

已知函数.
（Ⅰ）设，若在上单调递增，求实数的取值范围；
（Ⅱ）求证：存在，使.

在，，，这三个函数中，当时，使＞恒成立的函数的个数是（ ）

A．0个

B．1个

C．2个

D．3个

（1）函数f（x）=log_a（2x﹣1）﹣1的图象过定点（1，0）；
（2）已知函数f（x）是定义在R上的偶函数，当x≤0时，f（x）=x（x+1），则f（x）的解析式为f（x）=x²﹣|x|；
（3）若log_a＞1，则a的取值范围是（，1）；
（4）若2^﹣x﹣2^y＞lnx﹣ln（﹣y）（x＞0，y＜0），则x+y＜0．
其中所有正确命题的序号是       ．

已知函数f（x）=2x²﹣（a+2）x+a．
（Ⅰ）当a＞0时，求关于x的不等式f（x）＞0解集；
（Ⅱ）当x＞1时，若f（x）≥﹣1恒成立，求实数a的最大值．

记函数（，，均为常数，且）．
（1）若，（），求的值；
（2）若，时，函数在区间上的最大值为，求．

（本题8分）设二次，不等式的解集是．
（1）求；
（2）当函数的定义域是时，求函数的最大值．

已知二次函数满足条件，及．
（1）求的解析式；
（2）求在上的最值．