高中数学二次剩余解答题

进货原价为80元的商品400个，按90元一个售出时，可全部卖出。已知这种商品每个涨价一元，其销售数就减少20个，问售价应为多少时所获得利润最大？

已知函数 
（1）当时，求函数的最大值和最小值；
（2）求实数的取值范围，使在区间上是单调减函数

已知, 分别是方程的两个根，求角．

（本小题满分12分）定义在实数R上的函数y= f（x）是偶函数，当x≥0时，.
（Ⅰ）求f（x）在R上的表达式；
（Ⅱ）求y=f（x）的最大值，并写出f（x）在R上的单调区间（不必证明）.

。直线l₂与函数的图象以及直线l₁、l₂与函数的图象
围成的封闭图形如图中阴影所示，设这两个阴影区域的面积之和为
（１）求函数的解析式；
（２）若函数，判断是否存在极值，若存在，求出极值，若不存在，说明理由；

（本小题满分15分） 已知函数（其中
为锐角三角形的内角）且满足．
（1）求的值；
（2）若恒成立，求的取值范围．

一根弹簧，挂的物体时，长20 cm．在弹性限度内，所挂物体的重量每增加，弹簧就伸长cm．试写出弹簧的长度（cm）与所挂物体重量之间的关系的方程．

（本小题满分12分）
已知函数，
（1）当时，求的最大值和最小值
（2）若在上是单调函数，且，求的取值范围

（本小题满分12分）已知二次函数f（x）满足：函数f（x+1）为偶函数，f（x）的最小值为-4，函数f（x）的图象与x轴交点为A、B，且AB=4，求二次函数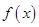的解析式．

已知二次函数y＝f(x)(x∈R)的图像是一条开口向下且对称轴为x＝3的抛物线，试比较大小：
(1)f(6)与f(4)

解不等式：－3＜4x－4x²≤0

(本小题满分12分)
已知函数，若对一切恒成立．求实数 的取值范围．(16分)

命题方程有两个不等的正实数根，命题方程无实数根。若“或”为真命题，求的取值范围。

已知二次函数的二次项系数为a，且不等式f(x)>-2x的解集为（-1，3）。
（1）若方程有两个相等的实数根，求的解析式；
（2）若函数在区间内单调递减，求a的取值范围；

已知，求的最小值。