高中数学二次剩余解答题

已知函数
（1）如果求a的值
（2）问a为何值时，函数的最小值为-4

已知二次函数满足．
（1）求的解析式；
（2）若在上有最小值，最大值，求a的取值集合．

（本小题满分12分）已知二次函数满足，且．
（1）求的解析式；
（2）若函数的最小值为，求实数的值；
（3）若对任意互不相同的，都有成立，求实数的取值范围．

（本题8分）设二次，不等式的解集是．
（1）求；
（2）当函数的定义域是时，求函数的最大值．

（本小题满分10分）函数f（x）＝4x²－4ax＋a²－2a＋2在区间[0,2]上有最小值3，求a的值．

（本小题满分14分）已知二次函数的图象过点，且函数是偶函数．
（1）求的解析式；
（2）已知,，求函数在上的最大值和最小值；
（3）函数的图象上是否存在这样的点，其横坐标是正整数，纵坐标是一个完全平方数？如果存在，求出这样的点的坐标；如果不存在，请说明理由．

（1）已知是一次函数，且满足，求的解析式；
（2）已知函数满足，求的解析式。

函数在闭区间上的最小值记为
（1）求的函数表达式；
（2）作的图像，并写出的最小值．

已知直线为函数的图像，曲线C为二次函数的图像，直线与曲线C交于不同两点A,B
（I）当时，求弦AB的长；
（II）求线段AB中点的轨迹方程；
（III）试利用抛物线的定义证明：曲线C为抛物线.

定义区间的区间长度为，如图是某圆拱形桥一孔圆拱的示意图．这个圆的圆拱跨度，拱高，建造时每间隔需要用一根支柱支撑，求支柱的高度所处的区间．（要求区间长度为）

已知函数，若，求实数的值．

（本小题满分12分）已知二次函数f（x）满足：函数f（x+1）为偶函数，f（x）的最小值为-4，函数f（x）的图象与x轴交点为A、B，且AB=4，求二次函数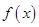的解析式．

已知函数
（1）当时，求函数的最大值和最小值；
（2）求实数的取值范围，使在区间上是单调函数

已知二次函数的图象如图．

（1）求它的对称轴与轴交点D的坐标；
（2）将该抛物线沿它的对称轴向上平移，设平移后的抛物线与轴，轴的交点分别为A、B、C三点，若∠ACB=90°，求此时抛物线的解析式；
（3）设（2）中平移后的抛物线的顶点为M，以AB为直径，D为圆心作⊙D，试判断直线CM与⊙D的位置关系，并说明理由．

设二次函数 (,)，
满足条件：①当时，，且；
②当时，；
③f(x)在R上的最小值为0.
求最大值m()，使得存在，只要，就有.