高中数学二次剩余试题

已知函数（）．
（1）若的定义域和值域均是，求实数的值；
（2）若对任意的，，总有，求实数的取值范围．

已知函数f(x)＝－x²＋2ax＋1－a在x∈[0,1]时有最大值2，求a的值．

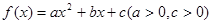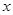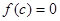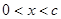已知二次函数的图像与轴有两个不同的公共点，且有，当时，恒有、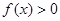
（1）试比较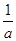与c的大小；
（2）试求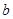的取值范围；
（3）若以二次函数的图像与坐标轴的三个交点为顶点的三角形的面积为5，求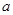的取值范围

已知二次函数的导函数为，且＞0，的图象与x
轴恰有一个交点，则的最小值为 ( 　 )

A．3

B．

C．2

D．

设函数．
（1）当时，记函数在[0，4]上的最大值为，求的最小值；
（2）存在实数，使得当时，恒成立，求的最大值及此时的值．

（本小题满分12分）
已知函数.
（Ⅰ）当时，求关于的不等式解集；
（Ⅱ）当时，若恒成立，求实数的最大值.

已知二次函数+的图象通过原点，对称轴为，．是的导函数，且 ．
（1）求的表达式（含有字母）；
（2）若数列满足，且，求数列的通项公式；
（3）在（2）条件下，若，，是否存在自然数，使得当时恒成立?若存在，求出最小的；若不存在，说明理由．

已知二次函数y＝f(x)的顶点坐标为，且方程f(x)＝0的两个实根之差的绝对值等于7，则此二次函数的解析式是________．

已知函数
（1）当时，求函数的最大值和最小值；
（2）求实数的取值范围，使在区间上是单调函数

已知二次函数的图象如图．

（1）求它的对称轴与轴交点D的坐标；
（2）将该抛物线沿它的对称轴向上平移，设平移后的抛物线与轴，轴的交点分别为A、B、C三点，若∠ACB=90°，求此时抛物线的解析式；
（3）设（2）中平移后的抛物线的顶点为M，以AB为直径，D为圆心作⊙D，试判断直线CM与⊙D的位置关系，并说明理由．

已知二次函数f（x）=
（1）若f（0）>0，求实数p的取值范围
（2）在区间［－1，1］内至少存在一个实数c，使f（c）>0，求实数p的取值范围。

（本小题满分12分）
已知函数.
（Ⅰ）当时，求关于的不等式解集；
（Ⅱ）当时，若恒成立，求实数的最大值.

某种商品，现在定价p元，每月卖出n件，设定价上涨x成，每月卖出数量减少y成，每月售货总金额变成现在的z倍．
(1)用x和y表示z；
(2)设x与y满足y＝kx(0<k<1)，利用k表示当每月售货总金额最大时x的值；
(3)若y＝x，求使每月售货总金额有所增加的x值的范围．

已知二次函数f（x）=ax²+bx+c（a＞0）．
（Ⅰ）（i）若b=﹣2，且f（x）在（1，+∞）上为单调递增函数，求实数a的取值范围；
（ii）若b=﹣1，c=1，当x∈[0，1]时，|f（x）|的最大值为1，求实数a的取值范围；
（Ⅱ）若f（0）≥1，f（1）≥1，f（x）=0的有两个小于1的不等正根，求a的最小正整数值．

二次函数y=ax²+bx+c的图象如图2所示，则下列结论①abc<0，②b²-4ac>0，③2a+b>0，④a+b+c<0，⑤ x=0为方程ax²+bx+c=-2的一个解，其中正确的有 （   ）

A．2个

B．3个

C．4个

D．5个