如图,在杨辉三角形中,斜线 的上方从1按箭头所示方向可以构成一个“锯齿形”的数列:1,3,3,4,6,5,10, ,记此数列的前
的上方从1按箭头所示方向可以构成一个“锯齿形”的数列:1,3,3,4,6,5,10, ,记此数列的前 项之和为
项之和为 ,则
,则 的值为( )
的值为( )
| A.66 | B.153 | C.295 | D.361 |
将集合{ |
| 且
且 }中的元素按上小下大,左小右大的顺序排成如图的三角形数表,将数表中位于第
}中的元素按上小下大,左小右大的顺序排成如图的三角形数表,将数表中位于第 行第
行第 列的数记为
列的数记为 (
( ),则
),则 = .
= .
设函数f(x)= (x>0),观察:f1(x)=f(x)=
(x>0),观察:f1(x)=f(x)= , f2(x)=f(f1(x))=
, f2(x)=f(f1(x))= , f3(x)=f(f2(x))=
, f3(x)=f(f2(x))= , f4(x)=f(f3(x))=
, f4(x)=f(f3(x))= ……根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= .
……根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= .
把正整数按照下面的表格进行排列
| 1 |
3 |
6 |
10 |
15 |
21 |
…… |
| 2 |
5 |
9 |
14 |
20 |
…… |
…… |
| 4 |
8 |
13 |
19 |
…… |
…… |
…… |
| 7 |
12 |
18 |
…… |
…… |
…… |
…… |
| 11 |
17 |
…… |
…… |
…… |
…… |
…… |
| 16 |
…… |
…… |
…… |
…… |
…… |
…… |
| …… |
…… |
…… |
…… |
…… |
…… |
…… |
则排在第6行,第4列的数是_______________;
排在第 行,第
行,第 列(
列( )的数是______________
)的数是______________
把正整数按一定的规则排成了如图所示的三角形数表.

设 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行、从左往右数第
行、从左往右数第 个数,如
个数,如 .若
.若 ,则
,则 .
.
将自然数按如图排列,其中处于从左到右第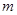 列从下到上第
列从下到上第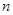 行的数记为
行的数记为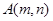 ,
,
如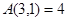 ,
,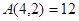 ,则
,则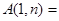 __________;
__________;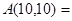 __________.
__________.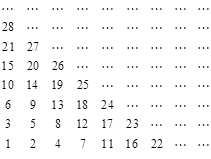
已知数列{an}的前n项和Sn,a1=﹣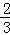 ,Sn+
,Sn+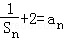 (n≥2).
(n≥2).
(1)计算S1,S2,S3,猜想Sn的表达式并用数学归纳法证明;
(2)设bn=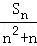 ,数列的{bn}的前n项和为Tn,求证:Tn>﹣
,数列的{bn}的前n项和为Tn,求证:Tn>﹣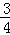 .
.
利用数学归纳法证明不等式 <f(n)(n≥2,n∈N*)的过程中,由n=k变到n=k+1时,左边增加了( )
<f(n)(n≥2,n∈N*)的过程中,由n=k变到n=k+1时,左边增加了( )
| A.1项 | B.k项 | C.2k-1项 | D.2k项 |
试题篮
()