规定A =x(x-1)…(x-m+1),其中x∈R,m为正整数,且A
=x(x-1)…(x-m+1),其中x∈R,m为正整数,且A =1,这是排列数A
=1,这是排列数A (n,m是正整数,且m≤n)的一种推广.
(n,m是正整数,且m≤n)的一种推广.
(1)求A 的值;
的值;
(2)排列数的性质:A =nA
=nA (其中m,n是正整数).问是否都能推广到A
(其中m,n是正整数).问是否都能推广到A (x∈R,m是正整数)的情形?若能推广,写出推广的形式,并且给予证明。
(x∈R,m是正整数)的情形?若能推广,写出推广的形式,并且给予证明。
用数学归纳法证明1+2+3+…+n2=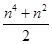 ,则当n=k+1时左端应在n=k的基础上加上( )
,则当n=k+1时左端应在n=k的基础上加上( )
| A.k2+1 |
| B.(k+1)2 |
C.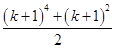 |
| D.(k2+1)+(k2+2)+…+(k+1)2 |
用数学归纳法证明(n+1)(n+2)…(n+n)=2n·1·3…(2n-1)(n∈N*)时,从“n=k到n=k+1”左边需增乘的代数式为( )
| A.2k+1 | B.2(2k+1) | C. |
D. |
已知数列 满足
满足 ,
,
(1)求 ,
, ,
, ,
, ;
;
(2)归纳猜想出通项公式 ,并且用数学归纳法证明;
,并且用数学归纳法证明;
(3)求证 能被15整除.
能被15整除.
在 中,不等式
中,不等式 成立;在四边形ABCD中,不等式
成立;在四边形ABCD中,不等式 成立;在五边形ABCDE中,不等式
成立;在五边形ABCDE中,不等式 成立
成立
 猜想在n边形
猜想在n边形 中,有不等式_______________________________成立.
中,有不等式_______________________________成立.
试题篮
()