高中数学第二数学归纳法选择题

用数学归纳法证明（）时，从“到”左边需增乘的代数式为（   ）

A．

B．

C．

D．

用数学归纳法证明“当n为正奇数时，xⁿ＋yⁿ能被x＋y整除”的第二步
是(  )．

A．假使n＝2k＋1时正确，再推n＝2k＋3正确

B．假使n＝2k－1时正确，再推n＝2k＋1正确

C．假使n＝k时正确，再推n＝k＋1正确

D．假使n≤k(k≥1)，再推n＝k＋2时正确(以上k∈N＋)

已知f(n)=(2n+7)·3ⁿ+9,存在自然数m,使得对任意n∈N^*,f(n)都能被m整除,则m的最大值为(　　)

A．18

B．36

C．48

D．54

用数学归纳法证明不等式1+++…+>(n∈N^*)成立,其初始值至少应取(　　)

A．7

B．8

C．9

D．10

已知n是正偶数,用数学归纳法证明时,若已假设n=k(k≥2且为偶数)时命题为真,则还需证明(　　)

A．n=k+1时命题成立

B．n=k+2时命题成立

C．n=2k+2时命题成立

D．n=2(k+2)时命题成立

在用数学归纳法证明凸n边形内角和定理时,第一步应验证(　　)

A．n=1时成立	B．n=2时成立
C．n=3时成立	D．n=4时成立

用数学归纳法证明（），在验证当n=1时，等式左边应为

A．1

B．1+a

C．1+a+a^2

D．1+a+a^2+a^3

用数学归纳法证明不等式，第二步由k到k+1时不等式左边需增加（      ）

A．	B．
C．	D．

用数学归纳法证明等式时，第一步验证时，左边应取的项是

A．1

B．

C．

D．

用数学归纳法证明不等式，第二步由k到k+1时不等式左边需增加（     ）

A．	B．
C．	D．

在用数学归纳法证明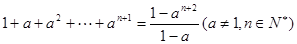时，在验证当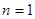时，等式左边为（   ）

A．1

B．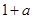

C．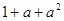

D．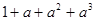

观察式子： ， ， ，……则可归纳出式子（）（   ）

A．	B．
C．	D．

用数学归纳法证明不等式“”的过程中，由n=k到n=k+1时,不等式的左边（   ）

A．增加了一项

B．增加了两项

C．增加了一项，又减少了一项

D．增加了两项，又减少了一项

用数学归纳法证明1＋a＋a²＋ ＋a^n＋1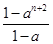＝ (n∈N^*，a≠1)，在验证n＝1时，左边所得的项为（　　）

A．1

B．1＋a＋a^2

C．1＋a

D．1＋a＋a^2＋a^3

已知n为正偶数，用数学归纳法证明 时，若已假设为偶数）时命题为真，则还需要用归纳假设再证（   ）时等式成立           （    ）

A．

B．

C．

D．