高中数学第二数学归纳法解答题

（本小题满分14分）在的展开式中，把叫做三项式系数．
（Ⅰ）当时，写出三项式系数的值；
（Ⅱ）二项式的展开式中，系数可用杨辉三角形数阵表示，如图：

当时，类似杨辉三角形数阵表，请列出三项式的次系数列的数阵表；
（Ⅲ）求的值（可用组合数作答）．

（本小题满分13分）如图，在一个可以向下和向右方无限延伸的表格中，将正偶数按已填好的各个方格中的数字显现的规律填入各方格中．其中第行，第列的数记作，，如．

2	4	8	14
6	10	16	24
12	18	26	36
20	28	38	50

（Ⅰ）写出的值；
（Ⅱ）若求的值；（只需写出结论）
（Ⅲ）设， （）， 记数列的前项和为，求；并求正整数，使得对任意，均有．

在数列{a_n}中，a₁＝，a_n＋1＝，求a₂、a₃、a₄的值，由此猜想数列{a_n}的通项公式，并用数学归纳法证明你的猜想．

观察下列等式
                                     第一个式子
                              第二个式子
                      第三个式子
               第四个式子
照此规律下去
（Ⅰ）写出第个等式；
（Ⅱ）你能做出什么一般性的猜想？请用数学归纳法证明猜想． 

（本题14分）某少数民族的刺绣有着悠久的历史，下图（1）、（2）、（3）、（4）为她们刺绣最简单的四个图案，这些图案都由小正方形构成，小正方形数越多刺绣越漂亮，现按同样的规律刺绣（小正方形的摆放规律相同），设第n个图形包含个小正方形.

（Ⅰ）求出；
（Ⅱ）利用合情推理的“归纳推理思想”归纳出与的关系式，
（Ⅲ）根据你得到的关系式求的表达式.

（本小题满分10分）已知多项式.
（Ⅰ）求及的值；
（Ⅱ）试探求对一切整数n，是否一定是整数？并证明你的结论．

（本小题满分10分）设个正数满足（且）．
（1）当时，证明：；
（2）当时，不等式也成立，请你将其推广到（且）个正数的情形，归纳出一般性的结论并用数学归纳法证明．

已知数列前项和且，
（1）试求
（2）猜想的表达式，并用数学归纳法证明猜想.

若a₁≤a₂≤…≤a_n，而b₁≥b₂≥…≥b_n或a₁≥a₂≥…≥a_n而b₁≤b₂≤…≤b_n，证明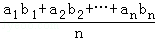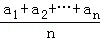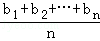：≤（）•（）．当且仅当a₁=a₂=…=a_n或b₁=b₂=…=b_n时等号成立．

设，其中为正整数．
（1）求，，的值；
（2）猜想满足不等式的正整数的范围，并用数学归纳法证明你的猜想．

给出四个等式：
1＝1
1－4＝－(1＋2)
1－4＋9＝1＋2＋3
1－4＋9－16＝－(1＋2＋3＋4)
……
（1）写出第5,6个等式，并猜测第n(n∈N^*)个等式
（2）用数学归纳法证明你猜测的等式．

是否存在常数，使等式对于一切都成立？若不存在，说明理由；若存在，请用数学归纳法证明？

给出四个等式：





（1）写出第个等式，并猜测第（）个等式；
（2）用数学归纳法证明你猜测的等式.

观察以下个等式：





照以上式子规律：
写出第个等式，并猜想第个等式；
用数学归纳法证明上述所猜想的第个等式成立．

用数学归纳法证明: