高中数学第二数学归纳法填空题

已知下列四个等式


依此类推，猜想第个等式为                                                   .

观察下列等式
1=1
2+3+4=9
3+4+5+6+7=25
4+5+6+7+8+9+10=49
照此规律，第个等式为                                            .

有下列各式：，，，……
则按此规律可猜想此类不等式的一般形式为：                        ．

观察下面的算式：
根据以上规律，把（为自然数且）写成这种和式形式，和式中最大的数为           ．

已知任意一个正整数的三次幂可表示成一些连续奇数的和，如图所示，可表示为，则我们把7、9、11叫做的“数因子”，若的一个“数因子”为，则       

观察下列等式：，，，， ，由以上等式推测出一个一般性的结论：对于N^*，___________．

观察系列等式，由以上等式推出一个一般性的结论：对于，              

如图，正方形边长为，分别作边上的三等分点，得正方形，再分别取边上的三等分点，得正方形，如此继续下去，得正方形，……，则正方形的面积为       ．

观察下列各式：，，，，，…，则_______．

设函数f（x）＝（x＞0），观察：f₁（x）＝f（x）＝, f₂（x）＝f（f₁（x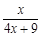））＝, f₃（x）＝f（f₂（x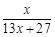））＝, f₄（x）＝f（f₃（x））＝……根据以上事实，由归纳推理可得：当n∈N*, n≥2时，f_n（x）＝f（_n－1（x））＝             ．

观察下列各式：
，
，
，
，
………………
第个式子是                                                ．

（1）若函数，且当且时，猜想的表达式　　　　　　　　　　　．
（2）用反证法证明命题＂若能被３整除，那么中至少有一个能被３整除＂时，假设应为　　　　　　　．

把正整数排列成如图甲三角形数阵,然后擦去第偶数行中的奇数和第奇数行中的偶数,得到如图乙的三角形数阵,再把图乙中的数按从小到大的顺序排成一列,得到一个数列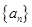,若,则________．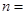

定义：分子为1且分母为正整数的分数叫做单位分数．我们可以把1拆分为无穷多个不同的单位分数之和．例如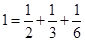：，，， 依此方法可得：，其中，则        ．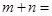

用数学归纳法证明1＋<n，其中n>1且n∈N^*，在验证n＝2时，式子的左边等于________．