高中数学西姆松定理解答题

如图，要计算西湖岸边两景点与的距离，由于地形的限制，需要在岸上选取和两点，现测得，，， ，，求两景点与的距离（精确到0.1km）．参考数据：  

（本小题满分10分）
在中，角所对的边分别为，向量，且．
（Ⅰ）求的值；  
（Ⅱ）若的面积为，求．

在△ABC中，已知角A为锐角，且.
（1）、将化简成的形式；
（2）、若，求边AC的长. ；

在中，角A、B、C所对的边分别为、、.已知向量，，且.
（Ⅰ） 求角的大小；
（Ⅱ） 若，求边的最小值.

△ABC的三个内角A、B、C成等差数列，分别为三个内角A、B、C所对的边，
求证：。  

（本小题满分12分）
在△ABC中，角A、B、C的对边分别为a、b、c，且－＝（2－）bc，sinA·sinB＝，BC边上中线AM的长为．
（Ⅰ）求角A和角B的大小；        
（Ⅱ）求△ABC的面积．

本小题满分12分）

港口A北偏东30°方向的C处有一检查站，港口正东方向的B处有一轮船，距离检查站为31海里，该轮船从B处沿正西方向航行20海里后到达D处观测站，已知观测站与检查站距离21海里，问此时轮船离港口A还有多远？

（本小题满分10分）7．
在中，角A、B、C的对边分别为a、b、c，已知，
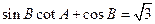，求b边的长。

三、解答题（本大题有5道小题，各小题12分，共60分）
17．在中，分别是角的对边，向量，，且 .
（1）求角的大小；
（2）设，且的最小正周期为，求在
区间上的最大值和最小值.

（本小题满分12分）
在△ABC中，角A、B、C的对边分别为a、b、c，且，
.
（1）求角A；
（2）设，求边的大小.

在⊿ABC中，BC=，AC=3，sinC=2sinA     
(I) 求AB的值：    
(II) 求sin的值

在中，，．
（1）求的值；
（2）设，求的面积．

（本小题满分12分）
港口A北偏东30°方向的C处有一检查站，港口正东方向的B处有一轮船，距离检查站为31海里，该轮船从B处沿正西方向航行20海里后到达D处观测站，已知观测站与检查站距离21海里，问此时轮船离港口A还有多远？

 （本小题满分12分）
已知中，角所对的边分别为又，:=2:3.
(1)求的值;         (2)若的边上的高为,求a的值.

 （本小题满分12分）
我缉私巡逻艇在一小岛A南偏西50º的方向，距小岛12海里的B处，发现隐藏在小岛边上的一走私船正开始向岛北偏西 10º方向行驶，测得其速度为每小时10海里，问我巡逻艇须用多大的速度朝什么方向航行才能恰在两小时后截获该走私船？（必要时，可参考下列数据sin38º≈0.62，）