高中数学三面角、直三面角的基本性质试题

若关于的实系数方程有两个根，一个根在区间内，另一根在区间内，记点对应的区域为S.那么区域S的面积是         .

对于大于1的自然数的次幂可用奇数
进行如图所示的“分裂”，仿此，记的“分裂”
中的最小数为，而的“分裂”中最大的数
是，则 _____.

本题共有2个小题，第1小题满分6分，第2小题满分10分．
某火山喷发停止后，为测量的需要，设距离喷口中心米内的圆环面为第区、米至米的圆环面为第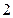区、……、第米至米的圆环面为第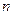区，…，现测得第区火山灰平均每平方米为1000千克、第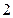区每平方米的平均重量较第区减少、第区较第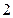区又减少，以此类推，求：
（1）离火山口1225米处的圆环面平均每平方米火山灰重量(结果精确到1千克)？
（2）第几区内的火山灰总重量最大？

已知是方程（是实常数）的一个根，是的反函数，则方程必有一根是              .

已知函数的零点，
则       .

方程的解为                  .

某农贸市场出售西红柿，当价格上涨时，
供给量相应增加，而需求量相应减少，
具体结果如下表：

单价（元）
供给量（）

表1  市场供给表

单价（元）
需求量（）

表2  市场需求表
根据以上提供的信息，市场供需平衡点（即供给量和需求量相等时的单价）大约为

A．元

B．元

C．元

D．元

（本小题满分12分）东海水晶制品厂去年的年产量为10万件,每件水晶产品的销售价格为100元，固定成本为80元.从今年起,工厂投入100万元科技成本,并计划以后每年比上一年多投入100万元科技成本.预计产量每年递增1万件,每件水晶产品的固定成本与科技成本的投入次数的关系是=.若水晶产品的销售价格不变,第次投入后的年利润为万元.①求出的表达式；②问从今年算起第几年利润最高？最高利润为多少万元？

甲方是一农场，乙方是一工厂。由于乙方生产需占用甲方的资源，因此甲方有权向乙方索赔，以弥补经济损失并获得一定净收入。在乙方不赔付甲方的情况下，乙方的年利润（元）与年产量（吨）满足关系。若乙方每生产一吨产品必须赔付甲方元（以下称为赔付价格）
⑴将乙方的实际年利润（元）表示为年产量（吨）的函数，并求乙方获得最大年利润时的年产量；
⑵甲方每年受乙方生产影响的经济损失金额为（元），在乙方按照获得最大年利润时的年产量的前提下，甲方要在索赔中获得最大净收入，应向乙方要求的赔付价格是多少？

某企业进行技术改造，有两种方案可供选择：甲方案--- 一次性贷款10万元，第一年可获利1万元，以后每年比前一年增加30%的利润 ；乙方案---每年贷款1万元，第一年可获利1万元，以后每年却比前一年增加利润5千元，两种方案使用期都是10年，到期一次性还本付息，若银行贷款利息均按年息10%的复利计算 ，试比较两种方案的优劣(计算时精确到千元，并取1.1

用长为16米的篱笆，借助墙角围成一个矩形ABCD(如图)，在P处有一棵树与两墙的距离分别为a米（0<a<12 ）和4米。若此树不圈在矩形外，求矩形ABCD面积的最大值M.

如图，江北水城湖畔有一块边长为2a的等边三角形的草坪，在这块草坪内安装灌溉水管DE，使DE把草坪分成面积相等的两部分，D在AB上，E在AC上.
①设AD = x（x≥0），DE = y，求y关于x的函数关系式；
②为节约成本，应如何安装，才能使灌溉水管DE最短，最短是多少？

比较下列各数 ， ， 的大小为