已知函数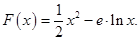
(I)求函数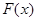 的极值;
的极值;
(II)对于函数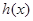 和
和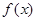 定义域内的任意实数
定义域内的任意实数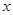 ,若存在常数
,若存在常数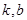 ,使得不等式
,使得不等式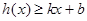 和
和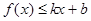 都成立,则称直线
都成立,则称直线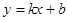 是函数
是函数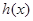 和
和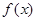 的“分界线”.
的“分界线”.
设函数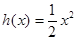 ,
,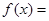
 ,试问函数
,试问函数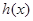 和
和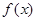 是否存在“分界线”?若存在,求出“分界线”的方程.若不存在请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程.若不存在请说明理由.
已知函数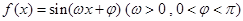 在一个周期内的部分对应值如下表:
在一个周期内的部分对应值如下表:
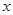 |
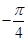 |
 |
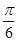 |
 |
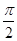 |
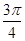 |
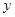 |
 |
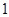 |
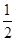 |
 |
 |
 |
(I)求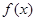 的解析式;
的解析式;
(II)设函数 ,
,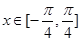 ,求
,求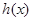 的最大值和最小值.
的最大值和最小值.
已知函数①f(x)=x2;②f(x)=ex;③f(x)=ln x;④f(x)=cos x.其中对于f(x)定义域内的任意一个x1都存在唯一的x2,使f(x1)f(x2)=1成立的函数是( )
| A.① | B.② | C.②③ | D.③④ |
已知函数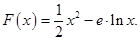
(I)求函数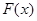 的最小值;
的最小值;
(II)对于函数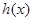 和
和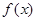 定义域内的任意实数
定义域内的任意实数 ,若存在常数
,若存在常数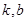 ,使得不等式
,使得不等式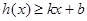 和
和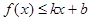 都成立,则称直线
都成立,则称直线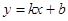 是函数
是函数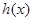 和
和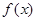 的“分界线”.
的“分界线”.
设函数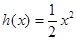 ,
,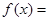
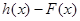 ,试问函数
,试问函数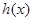 和
和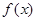 是否存在“分界线”?若存在,求出“分界线”的方程.若不存在请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程.若不存在请说明理由.
随着机构改革工作的深入进行,各单位要减员增效。有一家公司现有职员 人,(
人,( ,且
,且 为偶数),每人每年可创利
为偶数),每人每年可创利 万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年可多创利
万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年可多创利 万元,但公司需支付下岗职员每人每年
万元,但公司需支付下岗职员每人每年 万元的生活费,并且该公司正常运转所需人数不得小于现有员工的
万元的生活费,并且该公司正常运转所需人数不得小于现有员工的 ,为获得最大的经济效益,该公司应裁员多少人?
,为获得最大的经济效益,该公司应裁员多少人?
集合M={f(x)|存在实数t使得函数f(x)满足f(t+1)=f(t)+f(1)},则下列函数(a、b、c、k都是常数):
① y=kx+b(k≠0,b≠0);② y=ax2+bx+c(a≠0);
③ y=ax(0<a<1);④ y= (k≠0);⑤ y=sinx.
(k≠0);⑤ y=sinx.
其中属于集合M的函数是________.(填序号)
已知函数 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是 ,则不等式组
,则不等式组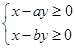 所确定的平面区域在
所确定的平面区域在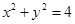 内的面积为 ( )
内的面积为 ( )
A. |
B.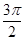 |
C.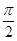 |
D.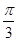 |
已知函数 f(x)=ax+lnx,其中a为常数,设e为自然对数的底数.
(1)当a=-1时,求 的最大值;
的最大值;
(2)若f(x)在区间(0,e]上的最大值为-3,求a的值;
(3)当a=-1时,试推断方程 是否有实数解 .
是否有实数解 .
已知两条直线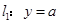 和
和 (其中
(其中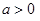 ),
), 与函数
与函数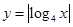 的图像从左至右相交于点
的图像从左至右相交于点 ,
,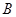 ,
,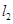 与函数
与函数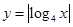 的图像从左至右相交于点
的图像从左至右相交于点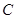 ,
,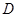 .记线段
.记线段 和
和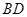 在
在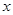 轴上的投影长度分别为
轴上的投影长度分别为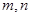 .当
.当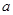 变化时,
变化时,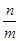 的最小值为( )
的最小值为( )
A.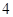 |
B.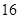 |
C.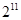 |
D.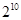 |
试题篮
()