已知函数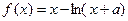 (
( 是常数)
是常数)
(I) 求函数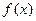 的单调区间;
的单调区间;
(II) 当 在
在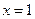 处取得极值时,若关于x的方程
处取得极值时,若关于x的方程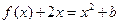 在
在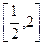 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数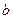 的取值范围;
的取值范围;
(III) 求证:当 时
时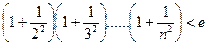 .
.
((本小题满分14分)
已知函数 满足
满足 当
当 ,当
,当 的最大值为
的最大值为 。
。
(1)求 时函数
时函数 的解析式;
的解析式;
(2)是否存在实数 使得不等式
使得不等式 对于
对于 若存在,求出实数
若存在,求出实数  的取值集合,若不存在,说明理由.
的取值集合,若不存在,说明理由.
(本小题满分14分)
已知定义域为 的函数
的函数 同时满足以下三个条件:
同时满足以下三个条件:
① 对任意的 ,总有
,总有 ≥0; ②
≥0; ② ;
;
③若 且
且 ,则有
,则有 成立,并且称
成立,并且称 为“友谊函数”,
为“友谊函数”,
请解答下列各题:
(1)若已知 为“友谊函数”,求
为“友谊函数”,求 的值;
的值;
(2)函数 在区间
在区间 上是否为“友谊函数”?并给出理由.
上是否为“友谊函数”?并给出理由.
(3)已知 为“友谊函数”,且
为“友谊函数”,且  ,求证:
,求证:
函数 的零点所在的区间为 ( )w.
的零点所在的区间为 ( )w.
.
| A.(-1,0) | B.(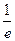 ,1) ,1) |
C.(1,2) | D.(1, ) ) |
为赢得2010年广州亚运会的商机,某商家最近进行了新科技产品的市场分析,调查显示,新产品每件成本9万元,售价为30万元,每星期卖出432件,如果降低价格,销售 量可以增加,且每星期多卖出的商品件数与商品单价的降低值
量可以增加,且每星期多卖出的商品件数与商品单价的降低值 (单位:万元,
(单位:万元, )的平方成正比,已知商品单价降低2万元时,一星期多卖出24件.(1)将一个星期的商品销售利润表示成
)的平方成正比,已知商品单价降低2万元时,一星期多卖出24件.(1)将一个星期的商品销售利润表示成 的函数;
的函数;
(2)如何定价才能使一个星期的商品销售利润最大?
试题篮
()