. (满分12分 )定义在
)定义在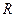 上的函数
上的函数 满足
满足 ,且
,且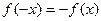
 ,当
,当 时,
时,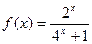 。1)求
。1)求 在
在 上的解析式;
上的解析式;
2)若 在
在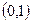 上是减函数,求函数
上是减函数,求函数 在
在 上的值域。
上的值域。
(本小题满分12分)
某房地产开发商投资8 1万元建一座写字楼,第一年装修费为1万元,以后每年增加2万元,把写字楼出租,每年收入租金30万元.
1万元建一座写字楼,第一年装修费为1万元,以后每年增加2万元,把写字楼出租,每年收入租金30万元.
(Ⅰ)若扣除投资和各种装修费,则从第几年开始获取纯利润?
(Ⅱ)若干年后开 发商为了投资其他项目,有两种处理方案:①年平均利润最大时以46万元出售该楼; ②纯利润总和最大时,以10万元出售该楼,问哪种方案盈利更多?
发商为了投资其他项目,有两种处理方案:①年平均利润最大时以46万元出售该楼; ②纯利润总和最大时,以10万元出售该楼,问哪种方案盈利更多?
(本小题满分13分)
已知定义域为R的函数 是奇函数.
是奇函数.
(1)求a的值;(2)判断 的单调性(不需要写出理由);
的单调性(不需要写出理由);
(3)若对任意的 ,不等式
,不等式 恒成立,求
恒成立,求 的取
的取 值范
值范 围.
围.
(本小题满分14分)
已知实系数一元二次方程x2+px+q=0的两根分别为x1,x2。
(1)若上述方程的一个根x1=4-i(i为虚数单位),求实数p,q的值;
(2)若方程的两根满足|x1|+|x2|=2,求实数p的取值范围。
(本小题满分14分)我国是水资源比较贫乏的国家之一,各地采用价格调控等手段以达到节约用水的目的.某市用水收费标准是:水费 基本费
基本费 超额费
超额费 定额损耗费,且有如下三条规定:① 若每月用水量不超过最低限量
定额损耗费,且有如下三条规定:① 若每月用水量不超过最低限量 立方米时,只付基本费9元和每户每月定额损耗费
立方米时,只付基本费9元和每户每月定额损耗费 元;② 若每月用水量超过
元;② 若每月用水量超过 立方米时,除了付基本费和定额损耗费外,超过部分每立方米付
立方米时,除了付基本费和定额损耗费外,超过部分每立方米付 元的超额费;③ 每户每月的定额损耗费
元的超额费;③ 每户每月的定额损耗费 不超过5元.
不超过5元.
(1) 求每户每月水费 (元)与月用水量
(元)与月用水量 (立方米)的函数关系;
(立方米)的函数关系;
(2) 该市一家庭今年第一季度每月的用水量和支付 的费用如下表所示:
的费用如下表所示:
| 月份 |
用水量(立方米) |
水费(元) |
| 一 |
4 |
17 |
| 二 |
5 |
23 |
| 三 |
2.5 |
11 |
试分析该家庭今年一、二、三各月份的用水量是否超过最低限量,并求 的值.
的值.
(生物体死亡后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”。
(1)根据这个规律,写出生物体内碳14的含量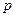 与死亡年数
与死亡年数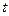
 之间的函数关系式。
之间的函数关系式。
(2)湖南长沙马王堆汉墓女尸出土时碳14的残余量约占原始含量的76.7℅,试推算马王堆汉墓的年代。(精确到个位;辅助数据: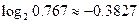 )
)
(本小题满分8分)
某交易市场的土豆在30天内每吨的交易价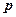 (千元)与时间
(千元)与时间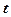 (天)(
(天)(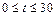 ),组成有序数对
),组成有序数对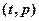 ,点
,点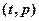 落在如图所示的两条线段上,该市场土豆在30天内的日交易量
落在如图所示的两条线段上,该市场土豆在30天内的日交易量 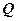 (吨)与时间
(吨)与时间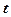 (天)的部分数据如下表所示
(天)的部分数据如下表所示
第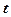 天 天 |
4 |
10 |
16 |
22 |
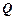 (吨) (吨) |
36 |
30 |
24 |
18 |
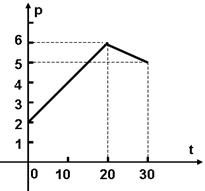
(1)根据提供的图象,写出每吨交易价格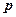 (千元)与时间
(千元)与时间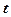 (天)所满足函数关系式;
(天)所满足函数关系式;
(2)根据表中数据确定日交易量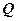 (吨)与时间
(吨)与时间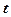 (天)的一次函数解析式;
(天)的一次函数解析式;
(3)用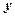 表示日交易额(千元),写出
表示日交易额(千元),写出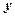 关于
关于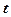 的函数解析式,问这30天中第几天交易额最大,最大值多少?
的函数解析式,问这30天中第几天交易额最大,最大值多少?
已知函数
 (
( 是常数),且
是常数),且 ,
, .
.
(1) 求 的值;
的值;
(2) 当 时,判断
时,判断 的单调性
的单调性 并证明;
并证明;
(3) 对任意的 ,若不等式
,若不等式

 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
试题篮
()