(本小题满分9分)要制做一个体积为72 的长方体带盖箱子,并且使长宽之比为
的长方体带盖箱子,并且使长宽之比为 ,设箱子的表面积为
,设箱子的表面积为 ,宽为
,宽为 。
。
(1)写出箱子的表面积 关于宽
关于宽 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;
(2)求箱子的表面积的最小值及取得最小值时的 的值。
的值。
(本小题满分12分)
设函数 其中实
其中实 数
数 。
。
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)当函数 与
与 的图象只有一个公共点时,记
的图象只有一个公共点时,记 的最小值为
的最小值为 ,求
,求 的值域;
的值域;
(Ⅲ)若 与
与 在区间
在区间 内均
内均 为增函数,求
为增函数,求 的取值范围
的取值范围
已知二次函数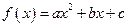 和“伪二次函数”
和“伪二次函数”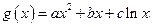 (
(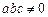 ),
),
(1)证明:只要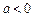 ,无论
,无论 取何值,函数
取何值,函数 在定义域内不可能总为增函数;
在定义域内不可能总为增函数;
(2)在同一函数图像上任意取不同两点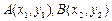 ,线段
,线段 中点为
中点为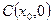 ,记直线
,记直线 的斜率为
的斜率为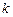 ,
,
1对于二次函数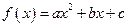 ,求证:
,求证: ;
;
2对于“伪二次函数”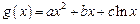 ,是否有1同样的性质?证明你的结论.
,是否有1同样的性质?证明你的结论.
(本小题满分16分)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是等腰梯形,其中高0.5米,AB=1米, CD=2a(a> )米.上部CmD是个半圆,固定点E为CD的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和CD平行的伸缩横杆.
)米.上部CmD是个半圆,固定点E为CD的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和CD平行的伸缩横杆.
(1)设MN与AB之间的距离为x米,试将三角通风窗EMN的通风面积S(平方米)表示成关于x的函数 ;
;
(2)当MN与AB之间的距离为多少米时,三角通风窗EMN的通风面积最大?并求出这个最大面积.
对于在区间 上有意义的两个函数
上有意义的两个函数 ,如果对任意
,如果对任意 均有
均有 ,则称
,则称 在
在 上是接近的,否则称
上是接近的,否则称 在
在 上是非接近的,现有两个函数
上是非接近的,现有两个函数 ,给定区间
,给定区间 .
.
(1)若 在给定区间
在给定区间 上都有意义,求
上都有意义,求 的取值范围;
的取值范围;
(2)讨论 在给定区间
在给定区间 上是否是接近的?
上是否是接近的?
本题共有2个小题,第 1小题满分6分,第2小题满分10分.
1小题满分6分,第2小题满分10分.
某火山喷发停止后,为测量的需要,设距离喷口中心 米内的圆环面为第
米内的圆环面为第 区、
区、 米至
米至 米的圆环面为第
米的圆环面为第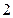 区、……、第
区、……、第 米至
米至 米的圆环面为
米的圆环面为 第
第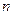 区,…,现测得第
区,…,现测得第 区火山灰平均每平方米为1000千克、第
区火山灰平均每平方米为1000千克、第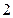 区每平方米的平均重量较第
区每平方米的平均重量较第 区减少
区减少 、第
、第 区较第
区较第 区又减少
区又减少
 ,以此类推,求:
,以此类推,求:
(1)离火山口1225米处的圆环面平均每平方米火山灰重量(结果精确到1千克)?
(2)第几区内的火 山灰总重量最大?
山灰总重量最大?
(本小题满分12分)东海水晶制品厂去年的年产量为10万件,每件水晶产品的销售价格为100元,固定成本为80元.从今年起,工厂投入100万元科技成本,并计划以后每年比上一年多投入100万元科技成本.预计产量每年递增1万件,每件水晶产品的固定成本 与科技成本的投入次数
与科技成本的投入次数 的关系是
的关系是 =
= .若
.若 水晶产品的销售价格不
水晶产品的销售价格不 变,第
变,第 次投入后的年利润为
次投入后的年利润为 万元.①求出
万元.①求出 的表达式;②问从今年算起第几年利润最高?最高利润为多少万元?
的表达式;②问从今年算起第几年利润最高?最高利润为多少万元?
甲方是一农场,乙方是一工厂。由于乙方生产需占用甲方的资源,因此甲方有权向乙方索赔,以弥补经济损失并获得一定净收入。在乙方不赔付甲方的情况下,乙方的年利润 (元)与年产量
(元)与年产量 (吨)满足关系
(吨)满足关系 。若乙方每生产一吨产品必须赔付甲方
。若乙方每生产一吨产品必须赔付甲方 元(以下称
元(以下称 为赔付价格)
为赔付价格)
⑴将乙方的实际年利润 (元)表示为年产量
(元)表示为年产量 (吨)的函数,并求乙方获得最大年利润时的年产量;
(吨)的函数,并求乙方获得最大年利润时的年产量;
⑵甲方每年受乙方生产影响的经济损失金额为 (元),在乙方按照获得最大年利润时的年产量的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格
(元),在乙方按照获得最大年利润时的年产量的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格 是多少?
是多少?
某企业进行技术改造,有两种方案可供选择:甲方案--- 一次性贷款10万元,第一年可获利1万元,以后每年比前一年增加30%的利润 ;乙方案---每年贷款1万元,第一年可获利1万元,以后每年却比前一年增加利润5千元,两种方案使用期都是10年,到期一次性还本付息,若银行贷款利息均按年息10%的复利计算 ,试比较两种方案的优劣(计算时精确到千元,并取1.1
用长为16米的篱笆,借助墙角围成一个矩形ABCD(如图),在P处有一棵树与两墙的距离分别为a米(0<a<12 )和4米。若此树不圈在矩形外,求矩形ABCD面积的最大值M.
试题篮
()