((本小题12分)
已知指数函数 满足:g(2)=4,定义域为
满足:g(2)=4,定义域为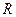 的函数
的函数 是奇函数。
是奇函数。
(1)确定 的解析式;
的解析式;
(2)求m,n的值;
(3)若对任意的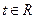 ,不等式
,不等式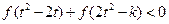 恒成立,求实数
恒成立,求实数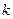 的取值范围。
的取值范围。
((本小题12分)
经市场调查,某超市的一种小商品在过去的近20天内的销售量(件)与价格(元)均为时间t(天) 的函数,且销售量近似满足g(t)=80-2t,价格近似满足f(t)=20-
的函数,且销售量近似满足g(t)=80-2t,价格近似满足f(t)=20- |t-10|.
|t-10|.
(1)试写出该种商品的日销售额y与时间t(0≤t≤20)的函数表达式;
(2)求该种商品的日销售额y的最大值与最小值.
.函数 (
( 为实常数).
为实常数).
(1)若 ,求
,求 的单调区间;
的单调区间;
(2)若 ,设
,设 在区间
在区间 的最小值为
的最小值为 ,求
,求 的表达式
的表达式
.(本小题满分12分)设函数 的定义域为R,当
的定义域为R,当 时,
时, ,且对任意实数
,且对任意实数 ,都有
,都有 成立,数列
成立,数列 满足
满足 且
且
(1)求 的值;
的值;
(2)若不等式 对一切
对一切 均成立,求
均成立,求 的最大值.
的最大值.
.已知指数函数 满足:g(2)=4,定义域为
满足:g(2)=4,定义域为 的函数
的函数 是奇函数。
是奇函数。
(1)确 定
定 的解析式;
的解析式;
(2)求m,n的值;
(3) 若对任意的
若对任意的 ,不等式
,不等式 恒成立,求实
恒成立,求实 数
数 的取值范围。
的取值范围。
(本小题满分12分)
如图:A、B两城相距100 km,某天燃气公司计划在两地之间建一天燃气站D 给A、B两城供气. 已知D地距A城x km,为保证城市安全,天燃气站距两城市的距离均不得少于10km . 已知建设费用y (万元)与A、B两地的供气距离(km)的平方和成正比,当天燃气站D距A城的距离为40km时, 建设费用为1300万元.(供气距离指天燃气站距到城市的距离)
(1)把建设费用y(万元)表示成供气距离x (km)的函数,并求定义域;
(2)天燃气供气站建在距A城多远,才能使建设供气费用最小.,最小费用是多少?
某市电力公司在电力供大于求时期为了鼓励居民用电,采用分段计费方法计算电费,每月用电不超过100度时,按每度0.57元计费;每月用电超过100度时,其中的100度仍按原标准收费,超过部分按每度0.5元计费.
(1)设每月用电x度,应交电费y元,写出y关于x的函数关系.
(2)小王家第一季度共用了多少度电?
| 月份 |
1月份 |
2月份 |
3月份 |
合计 |
| 缴费金额 |
76元 |
63元 |
45元6角 |
184元6角 |
问:小王家第一季度共用了多少度电?
试题篮
()