设命题p:函数f(x)=lg(ax2-4x+a)的定义域为R;命题q:不等式2x2+x>2+ax,在x∈(-∞,-1)上恒成立,如果命题“p∨q”为真命题,命题“p∧q”为假命题,求实数a的取值范围.
已知命题p:m∈R,且m+1≤0,命题q:∀x∈R,x2+mx+1>0恒成立,若p∧q为假命题,则m的取值范围是________.
已知函数f(x)在区间(-∞,+∞)上是增函数,a,b∈R.
(1)求证:若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b);
(2)判断(1)中命题的逆命题是否正确,并证明你的结论.
下列命题中假命题有 ( )
①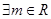 ,使
,使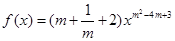 是幂函数;
是幂函数;
②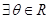 ,使
,使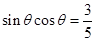 成立;
成立;
③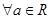 ,使
,使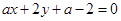 恒过定点;
恒过定点;
④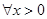 ,不等式
,不等式 成立的充要条件
成立的充要条件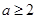 .
.
| A.3个 | B.2个 | C.1个 | D.0个 |
下列结论中正确的是 (填上所有正确结论得序号)
(填上所有正确结论得序号)
①对于函数 ,若
,若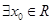 ,使得
,使得 ,则函数
,则函数 关于直线
关于直线 对称;
对称;
②函数 有2个零点;
有2个零点;
③若关于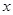 的不等式
的不等式 的解集为
的解集为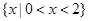 ,则
,则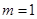 ;
;
④已知随机变量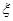 服从正态分布
服从正态分布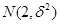 且
且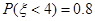 ,则
,则 ;
;
⑤等比数列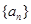 的前
的前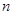 项和为
项和为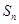 ,已知
,已知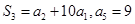 ,则
,则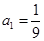
下列有关命题的说法正确的是( )
A.命题“若 ”的否命题为:“若 ”的否命题为:“若 ”; ”; |
B.“ ”是“ ”是“ ”的必要不充分条件; ”的必要不充分条件; |
C.命题“  ,使得 ,使得 ”的否定是:“ ”的否定是:“  ,均有 ,均有 ”; ”; |
D.命题“若 ”的逆否命题为真命题. ”的逆否命题为真命题. |
已知c>0,设命题p:函数y=cx为减函数.命题q:当x∈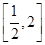 时,函数f(x)=x+
时,函数f(x)=x+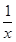 >
> 恒成立.如果p或q为真命题,p且q为假命题,求c的取值范围.
恒成立.如果p或q为真命题,p且q为假命题,求c的取值范围.
下列结论:
①若命题p:∃x0∈R,tan x0=2;命题q:∀x∈R,x2-x+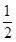 >0.则命题“p∧(
>0.则命题“p∧(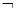 q)”是假命题;
q)”是假命题;
②已知直线l1:ax+3y-1=0,l2:x+by+1=0,则l1⊥l2的充要条件是 =-3;
=-3;
③“设a、b∈R,若ab≥2,则a2+b2>4”的否命题为:“设a、b∈R,若ab<2,则a2+b2≤4”.
其中正确结论的序号为________.
已知命题p:“∀x∈N*,x> ”,命题p的否定为命题q,则q是“________”;q的真假为________(填“真”或“假”).
”,命题p的否定为命题q,则q是“________”;q的真假为________(填“真”或“假”).
若命题“∃x∈R,使得x2+(a-1)x+1≤0”为假命题,则实数a的取值范围是________.
已知集合A={x|x2-4mx+2m+6=0},B={x|x<0},若命题“A∩B=∅”是假命题,求实数m的取值范围.
给出下列命题:
①函数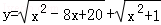 的最小值为5;
的最小值为5;
②若直线y=kx+1与曲线y=|x|有两个交点,则k的取值范围是﹣1≤k≤1;
③若直线m被两平行线l1:x﹣y+1=0与l2:x﹣y+3=0所截得的线段的长为2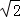 ,则m的倾斜角可以是15°或75°
,则m的倾斜角可以是15°或75°
④设Sn是公差为d(d≠0)的无穷等差数列{an}的前n项和,若对任意n∈N*,均有Sn>0,则数列{Sn}是递增数列
⑤设△ABC的内角A.B.C所对的边分别为a,b,c,若三边的长为连续的三个正整数,且A>B>C,3b=20acosA则sinA:sinB:sinC为6:5:4
其中所有正确命题的序号是 .
设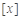 表示不超过
表示不超过 的最大整数,如
的最大整数,如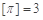 ,
,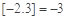 .给出下列命题:
.给出下列命题:
①对任意实数 ,都有
,都有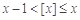 ;
;
②对任意实数 、
、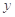 ,都有
,都有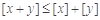 ;③
;③ ;
;
④若函数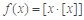 ,当
,当 时,令
时,令 的值域为A,记集合A的元素个数为
的值域为A,记集合A的元素个数为 ,则
,则 的最小值为
的最小值为 .
.
其中所有真命题的序号是_________________.
[2014·孝感统考]已知命题p:∃x∈R,使sinx= ;命题q:∀x∈R,都有x2+x+1>0.给出下列结论:
;命题q:∀x∈R,都有x2+x+1>0.给出下列结论:
①命题p∧q是真命题;②命题( p)∨q是真命题;③命题(
p)∨q是真命题;③命题( p)∨(
p)∨( q)是假命题;④命题p∧(
q)是假命题;④命题p∧( q)是假命题.
q)是假命题.
其中正确的是( )
| A.②③ | B.②④ | C.③④ | D.①②③ |
试题篮
()