高中数学表面展开图试题

三棱锥的四个顶点都在球面上，SA是球的直径，，，则该球的表面积为（    ）

A．

B．

C．

D．

如图,四棱锥P-ABCD中,底面ABCD为正方形,DA⊥面ABP,AB=1,PA=2,∠PAB=60°.
(1)求证:平面PBC⊥面PDC
(2)设E为PC上一点,若二面角B-EA-P的余弦值为-,求三棱锥E-PAB的体积.

如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，且CE∥AB.
（1）求证：CE⊥平面PAD；
（2）若PA=AB=1，AD=3，CD=，∠CDA=45°，求四棱锥P-ABCD的体积.

如图，在三棱锥中，是边长为4的正三角形，平面平面，，为的中点.

（1）证明：；
（2）求二面角的余弦值；
（3）求点到平面的距离.

设△ABC的三边长分别为a、b、c，△ABC的面积为S，内切圆半径为r，则r＝；类比这个结论可知：四面体S－ABC的四个面的面积分别为S₁、S₂、S₃、S₄，内切球的半径为r，四面体S－ABC的体积为V，则r＝(　 　)

A．

B．

C．

D．

如图,四棱柱 $ABCD-A_1{B}_1{C}_1{D}_1$的底面 $ABCD$是正方形, $O$为底面中心, $A_{1}O\perp$平面 $ABCD$, $AB=A{A}_1=\sqrt{2}$.

（1）证明:  $A_{1}BD//$平面 $C{D}_1{B}_1$;
（2）求三棱柱 $ABD-A_1{B}_1{D}_1$的体积.

已知矩形的顶点都在半径为4的球的球面上，且,则棱锥的体积为。

已知的周长为，面积为，则的内切圆半径为 ．将此结论类比到空间，已知四面体的表面积为，体积为，则四面体的内切球的半径     ．

在如图所示的多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，且AC＝AD＝CD＝DE＝2，AB＝1.

(1)请在线段CE上找到点F的位置，使得恰有直线BF∥平面ACD，并证明这一结论；
(2)求多面体ABCDE的体积．

如图甲，在平面四边形ABCD中，已知,，现将四边形ABCD沿BD折起，使平面ABD平面BDC（如图乙），设点E，F分别为棱AC，AD的中点．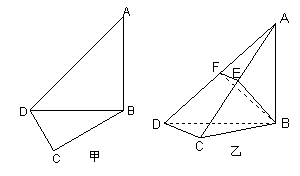

（1）求证：DC平面ABC；     
（2）设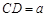，求三棱锥A－BFE的体积．

如图，三角形中，，是边长为的正方形，平面 ⊥底面，若、分别是、的中点．
（1）求证：∥底面；
（2）求证：⊥平面；
（3）求几何体的体积．

如图，已知正方体的棱长为2，E、F分别是、的中点，过、E、F作平面交于G．
(l)求证：EG∥；
(2)求二面角的余弦值；
(3)求正方体被平面所截得的几何体的体积．

如图，在直角梯形中，°，，平面，，，设的中点为，．

(1) 求证：平面；
(2) 求四棱锥的体积．

如图，等边三角形的中线与中位线相交于，已知是△绕旋转过程中的一个图形，下列命题中，错误的是(　　  )

A．动点在平面上的射影在线段上

B．恒有平面⊥平面

C．三棱锥的体积有最大值

D．异面直线与不可能垂直

如图，四边形ABCD是梯形，四边形CDEF是矩形，且平面ABCD⊥平面CDEF，∠BAD＝∠CDA＝90°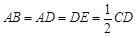，，M是线段AE上的动点．
（1）试确定点M的位置，使AC∥平面DMF，并说明理由；
（2）在（1）的条件下，求平面MDF将几何体ADE－BCF分成的两部分的体积之比．