设X为随机变量,从棱长为a的正方体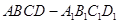 ,的八个顶点中任取四个点,当四点共面时,X=0;当四点不共面时,X的值为四点组成的四面体的体积.
,的八个顶点中任取四个点,当四点共面时,X=0;当四点不共面时,X的值为四点组成的四面体的体积.
(1)求概率P(X=0);
(2)求X的分布列,并求其数学期望E(X).
(本小题满分14分)如图,菱形 的边长为
的边长为 ,
, ,
, .将菱形
.将菱形 沿对角线
沿对角线 折起,得到三棱锥
折起,得到三棱锥 ,点
,点 是棱
是棱 的中点,
的中点, .
.
(1)求证: 平面
平面 ;
;
(2)求三棱锥 的体积.
的体积.
如图,四棱锥P-ABCD的底面是正方形,PD 面ABCD,E是PD上一点.
面ABCD,E是PD上一点.
(1)求证:AC BE.
BE.
(2)若PD=AD=1,且 的余弦值为
的余弦值为 ,求三棱锥E-PBC的体积.
,求三棱锥E-PBC的体积.
如图所示, 平面ABCD,四边形ABCD为正方形,且
平面ABCD,四边形ABCD为正方形,且 分别是线段PA、PD、CD、BC的中点.
分别是线段PA、PD、CD、BC的中点.
(1)求证:BC//平面EFG;
(2)求证: 平面AEG;
平面AEG;
(3)求三棱锥E-AFG与四棱锥P-ABCD的体积比.
已知一个几何体的三视图如图所示.
(Ⅰ)求此几何体的表面积;
(Ⅱ)在如图的正视图中,如果点 为所在线段中点,点
为所在线段中点,点 为顶点,求在几何体侧面上从点
为顶点,求在几何体侧面上从点 到点
到点 的最短路径的长.
的最短路径的长.
如图所示几何体是正方体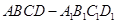 截去三棱锥
截去三棱锥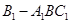 后所得,点
后所得,点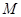 为
为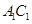 的中点.
的中点.
(1) 求证: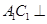 平面
平面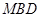 ;
;
(2) 当正方体棱长等于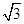 时,求三棱锥
时,求三棱锥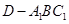 的体积.
的体积.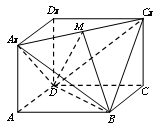
如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD且EF= BD.
BD.
(1)求证:BF∥平面ACE;
(2)求证:平面EAC⊥平面BDEF
(3)求几何体ABCDEF的体积.
三棱锥P−ABC中,PA⊥平面ABC,AB⊥BC。
(1)证明:平面PAB⊥平面PBC;
(2)若 ,
, ,PB与底面ABC成60°角,
,PB与底面ABC成60°角, 分别是
分别是 与
与 的中点,
的中点, 是线段
是线段 上任意一动点(可与端点重合),求多面体
上任意一动点(可与端点重合),求多面体 的体积.
的体积.
试题篮
()