高中数学选择题

为了解某班学生喜爱打篮球是否与性别有关，对该班50名学生进行了问卷调查，得到如下的2×2列联表．

	喜爱打篮球	不喜爱打篮球	合计
男生	20	5	25
女生	10	15	25
合计	30	20	50

 
则至少有（ ）的把握认为喜爱打篮球与性别有关．
A.95%    B.99%    C.99.5%    D.99.9%

以下四个命题中：
①从匀速传递的产品流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样；
②两个随机变量的线性相关性越强，相关系数的绝对值越接近于1；
③若数据x₁，x₂，x₃，…，x_n的方差为1，则2x₁，2x₂，2x₃，…，2x_n的方差为2；
④对分类变量X与Y的随机变量k²的观测值k来说，k越小，判断“X与Y有关系”的把握程度越大．
其中真命题的个数为（ ）

A．1

B．2

C．3

D．4

已知回归直线的斜率的估计值是1.23，样本点的中心为（4，5），则回归直线的方程是（ ）

A．=1.23x+4

B．=1.23x﹣0.08

C．=1.23x+0.8

D．=1.23x+0.08

在2013年9月15日，某市物价部门对本市的5家商场的某种商品的一天销售量及其价格进行调查，5家商场的售价x元和销售量y件之间的一组数据如下表所示：

价格x	9	9.5	10	10.5	11
销售量y	11	10	8	6	5

 
由散点图可知，销售量y与价格x之间有较好的线性相关关系，其线性回归方程是：y=﹣3.2x+a，则a=（ ）
A.﹣24    B.35.6    C.40.5    D.40

已知具有线性相关的两个变量x，y之间的一组数据如下：

x	0	1	2	3	4
y	2.2	4.3	4.5	4.8	6.7

 
且回归方程是=0.95x+a，则当x=6时，y的预测值为（ ）
A.8.0    B.8.1    C.8.2    D.8.3

经统计，用于数学学习的时间（单位：小时）与成绩（单位：分）近似于线性相关关系，对每小组学生每周用于数学的学习时间x与数学成绩y进行数据收集如下：

x	15	16	18	19	22
y	102	98	115	115	120

 
由表中样本数据求得回归方程为=kx+a，则点（a，b）与直线x+18y=100的位置关系是（ ）
A.点在直线左侧    B.点在直线右侧    C.点在直线上    D.无法确定

某产品在某零售摊位上的零售价x（单位：元）与每天的销售量y（单位：个）的统计资料如下表所示：

x	16	17	18	19
y	50	34	41	31

 
由上表，可得回归直线方程中的=﹣4，据此模型预计零售价定为15元时，每天的销售量为（ ）
A.48个    B.49个    C.50个   D.51个

已知x，y的值如表所示：

x	2	3	4
y	5	4	6

 
如果y与x呈线性相关且回归直线方程为，则b=（ ）
A.    B.    C.    D.

我区前n年参加社会实践学生总数S_n与n之间的关系如图所示，从目前记录的结果看，前m年的年平均人数最高，m的值为（ ）

A．5

B．7

C．9

D．11

在一次实验中，测得（x，y）的四组值为（1，2），（2，3），（3，4），（4，5），则y与x之间的回归直线方程为（ ）

A．=x+1

B．=x+2

C．=2x+1

D．=x﹣1

已知x、y取值如下表：

x	0	1	4	5	6	8
y	1.3	1.8	5.6	6.1	7.4	9.3

 
从所得的散点图分析可知：y与x线性相关，且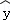=0.95x+a，则a=（ ）
A.1.30    B.1.45    C.1.65   D.1.80

对具有线性相关关系的变量x，y，有一组观测数据（x_i，y_i）（i=1，2，…，8），其回归直线方程是：=x+a，且x₁+x₂+x₃+…+x₈=3（y₁+y₂+y₃+…+y₈）=6，则实数a的值是（ ）

A．

B．

C．

D．

为研究语文成绩和英语成绩之间是否具有线性相关关系，统计两科成绩得到如图所示的散点图（两坐标轴单位长度相同），用回归直线=bx+a近似的刻画其相关关系，根据图形，以下结论最有可能成立的是（ ）

A．线性相关关系较强，b的值为1.25

B．线性相关关系较强，b的值为0.83

C．线性相关关系较强，b的值为﹣0.87

D．线性相关关系太弱，无研究价值

如图是根据变量x，y的观测数据（x_i，y_i）（i=1，2，…10）得到的散点图，由这些散点图可以判断变量x，y具有相关关系的图是（ ）

A．①②

B．①④

C．②③

D．③④

观察下列关于变量x和y的三个散点图，它们从左到右的对应关系依次是（ ）

A．正相关、负相关、不相关

B．负相关、不相关、正相关

C．负相关、正相关、不相关

D．正相关、不相关、负相关