高中数学解答题

已知的展开式前三项中的的系数成等差数列.
　（1）展开式中所有的的有理项为第几项？
　（2）求展开式中系数最大的项.

为考查某种药物预防疾病的效果,进行动物试验,得到如下丢失数据的列联表:
药物效果试验列联表

	患病	未患病	总计
没服用药	20	30	50
服用药	x	y	50
总计	M	N	100

设从没服用药的动物中任取两只,未患病数为X;从服用药物的动物中任取两只,未患病数为Y,工作人员曾计算过P(X=0)=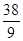 P(Y=0).
(1)求出列联表中数据x,y,M,N的值;
(2)能够有多大的把握认为药物有效?
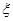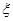(3)现在从该100头动物中,采用随机抽样方法每次抽取1头,抽后返回，抽取5次, 若每次抽取的结果是相互独立的，记被抽取的5头中为服了药还患病的数量为.,求的期望E(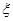)和方差D().
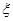参考公式：（其中）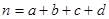

P(K^2≥k)	0.25	0.15	0.10	0.05	0.010	0.005
k	1.323	2.072	2.706	3.845	6.635	7.879

在1，2，3，…，9这9个自然数中，任取3个数，
(1)记Y表示“任取的3个数中偶数的个数”，求随机变量Y的分布列及其期望；
(2)记X为3个数中两数相邻的组数，例如取出的数为1，2，3，则有这两组相邻的数1，2和2，3，此时X的值为2，求随机变量X的分布列及其数学期望E(X).

已知函数（），该函数所表示的曲线上的一个最高点为，由此最高点到相邻的最低点间曲线与x轴交于点（6，0）。
（1）求函数解析式；
（2）求函数的单调区间；
（3）若，求的值域。

已知，。
（1）求的振幅，最小正周期，对称轴，对称中心。
（2）说明是由余弦曲线经过怎样变换得到。

已知,
(1)求与的夹角；  （2）求。

已知，计算：
（1）     （2）

已知，。
（1）求，；（2）若为单位向量，求的坐标。

如图，已知平面，平面，△为等边三角形，，为的中点．

（1）求证：平面；
（2）求证：平面平面；
（3）求直线和平面所成角的正弦值．

如图所示，校园内计划修建一个矩形花坛并在花坛内装置两个相同的喷水器。已知喷水器的喷水区域是半径为5m的圆。问如何设计花坛的尺寸和两个喷水器的位置，才能使花坛的面积最大且能全部喷到水？

已知函数f(x)＝|x＋1|，g(x)＝2|x|＋a.
(1)当a＝0时，解不等式f(x)≥g(x)；
(2)若任意x∈R，f(x)g(x)恒成立，求实数a的取值范围．

已知函数（e为自然对数的底数）．
（1）求函数的单调增区间；
（2）设不等式的解集为M，且集合，求实数t的取值范围．

已知为实数，函数．
(1) 若，求函数在[－，1]上的极大值和极小值；
(2)若函数的图象上有与轴平行的切线，求的取值范围．

设函数．
（1）求不等式的解集；
（2）若不等式的解集是非空的集合，求实数的取值范围．

某单位要建造一个长方体无盖贮水箱，其容积为48m³,深为3m，如果池底每1m²的造价为40元，池壁每1m²的造价为20元，问怎样设计水箱能使总造价最低，最低总造价是多少元？