已知椭圆 :
: 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切.
(1)求椭圆C的方程;
(2)设 ,
, 、
、 是椭圆
是椭圆 上关于
上关于 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆 于另一点
于另一点 ,求直线
,求直线 的斜率的取值范围;
的斜率的取值范围;
(3)在(2)的条件下,证明直线 与
与 轴相交于定点.
轴相交于定点.
在直角坐标系中,射线OA: x-y=0(x≥0),
OB: x+2y=0(x≥0),过点P(1,0)作直线分别交射线OA、OB于A、B两点.
(1)当AB中点为P时,求直线AB的方程;
(2)当AB中点在直线 上时,求直线AB的方程.
上时,求直线AB的方程.
已知四棱锥P-ABCD的直观图(如图(1))及左视图(如图(2)),底面ABCD是边长为2的正方形,平面PAB⊥平面ABCD,PA=PB。
(1)求证:AD⊥PB;
(2)求异面直线PD与AB所成角的余弦值;
(3)求平面PAB与平面PCD所成锐二面角的大小.
已知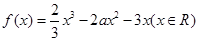 .
.
(Ⅰ) 时,求证
时,求证 在
在 内是减函数;
内是减函数;
(Ⅱ)若 在
在 内有且只有一个极值点,求实数
内有且只有一个极值点,求实数 的取值范围.
的取值范围.
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(Ⅰ)从袋中随机取出两个球,求取出的球的编号之和不大于4的概率;
(Ⅱ)先从袋中随机取一个球,该球的编号为 ,将球放回袋中,然后再从袋中随机取一个
,将球放回袋中,然后再从袋中随机取一个
球,该球的编号为 ,求
,求 的概率.
的概率.
作为绍兴市2013年5.1劳动节系列活动之一的花卉展在镜湖湿地公园举行.现有一占地1800平方米的矩形地块,中间三个矩形设计为花圃(如图),种植有不同品种的观赏花卉,周围则均是宽为1米的赏花小径,设花圃占地面积为 平方米,矩形一边的长为
平方米,矩形一边的长为 米(如图所示)
米(如图所示)
(1)试将 表示为
表示为 的函数;
的函数;
(2)问应该如何设计矩形地块的边长,使花圃占地面积 取得最大值.
取得最大值.
试题篮
()