高中数学解答题

已知函数,函数
⑴当时,求函数的表达式;
⑵若,函数在上的最小值是2 ,求的值;
⑶在⑵的条件下,求直线与函数的图象所围成图形的面积.

数列{a_n}满足：a₁=, 前n项和S_n=,
（1）写出a₂, a₃, a₄；（2）猜出a_n的表达式，并用数学归纳法证明.

设数列的前项和为，且.
（1）求
（2）求证：数列是等比数列；
（3）求数列的前项和.

为适应新课改，切实减轻学生负担，提高学生综合素质，某市某学校高三年级文科生300人在数学选修4-4、4-5、4-7选课方面进行改革，由学生自由选择2门（不可多选或少选），选课情况如下表：

	4-4	4-5	4-7
男生	130		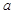80
女生		100	60

（1）为了解学生情况，现采用分层抽样方法抽取了三科作业共50本，统计发现4-5有18本，试根据这一数据求出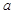，的值.
（2）为方便开课，学校要求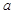≥110，＞110，计算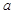＞的概率.

设函数，且以为最小正周期.
（1）求的值； 
（2）已知，求的值.

已知都是正数，且成等比数列，求证：

已知曲线C₁的极坐标方程为，曲线C₂的极坐标方程为，曲线C₁，C₂相交于A，B两点
（I）把曲线C₁，C₂的极坐标方程转化为直角坐标方程；
（II）求弦AB的长度．

已知函数的图像过坐标原点，且在点处的切线的斜率是．
（1）求实数的值；
（2）求在区间上的最大值；
（3）对任意给定的正实数，曲线上是否存在两点，使得是以为
直角顶点的直角三角形，且此三角形斜边的中点在轴上？请说明理由．

已知椭圆中心在原点，焦点在y轴上，焦距为4，离心率为．
（I）求椭圆方程；
（II）设椭圆在y轴的正半轴上的焦点为M，又点A和点B在椭圆上，且M分有向线段所成的比为2，求线段AB所在直线的方程．

已知的面积满足，且，与的夹角为.
（1）求的取值范围；
（2）求函数的最大值及最小值．

已知cosα=,cos(α+β)=,且α∈(π,),α+β∈(,2π),求β.

学校为了对某课题进行研究，用分层抽样方法从三个年级高一、高二、高三的相关老师中，抽取若干人组成研究小组，有关数据见下表(单位：人).

年级	相关人数	抽取人数
高一	18	x
高二	36	2
高三	54	y

 
(1)求x,y;
(2)若从高二、高三抽取的人中选2人做专题发言，求这2人都来自高三的概率。

已知函数．
（1）求证函数在区间上存在唯一的极值点，并用二分法求函数取得极值时相应的近似值（误差不超过）；（参考数据，，）
（2）当时，若关于的不等式恒成立，试求实数的取值范围.

设，在线段上任取两点（不含两端点），将线段分成了三条线段．
（1）若分成的三条线段的长度均为正整数，求这三条线段可以构成三角形的概率；
（2）若分成的三条线段的长度均为正实数，求这三条线段可以构成三角形的概率．

在△ABC中，内角A，B，C所对边长分别为，，，.
（1）求的最大值及的取值范围；
（2）求函数的最大值和最小值.