设A( ),B(
),B( )是椭圆
)是椭圆 的两点,
的两点, ,
, ,且
,且 ,椭圆的离心率
,椭圆的离心率 ,短轴长为2,O为坐标原点。
,短轴长为2,O为坐标原点。
(1)求椭圆方程;
(2)若存在斜率为 的直线AB过椭圆的焦点F(
的直线AB过椭圆的焦点F( )(
)( 为半焦距),求
为半焦距),求 的值;
的值;
(3)试问 AOB的面积是否为定值?若是,求出该定值;若不是,说明理由。
AOB的面积是否为定值?若是,求出该定值;若不是,说明理由。
(本小题满分10分)选修4-5:不等式选讲
函数
(1)画出函数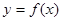 的图象;
的图象;
(2)若不等式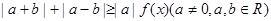 恒成立,求实数
恒成立,求实数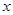 的范围.
的范围.
(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系中,直线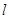 的参数方程为
的参数方程为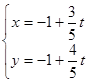 (
(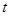 为参数).若以坐标原点
为参数).若以坐标原点 为极点,
为极点, 轴正半轴为极轴建立极坐标系,则曲线
轴正半轴为极轴建立极坐标系,则曲线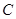 的极坐标方程为
的极坐标方程为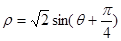 .
.
(1)求曲线C的直角坐标方程;
(2)求直线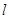 被曲线
被曲线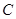 所截得的弦长.
所截得的弦长.
(本小题满分10分)选修4-1:几何证明与选讲
如图,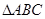 为直角三角形,
为直角三角形,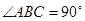 ,以
,以 为直径的圆交
为直径的圆交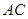 于点
于点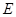 ,点
,点 是
是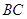 边的中点,连
边的中点,连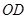 交圆
交圆 于点
于点 .
.
(1)求证: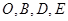 四点共圆;
四点共圆;
(2)求证: .
.
在极坐标系中,曲线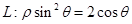 ,过点A(5,α)(α为锐角且
,过点A(5,α)(α为锐角且 )作平行于
)作平行于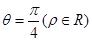 的直线
的直线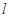 ,且
,且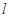 与曲线L分别交于B,C两点。
与曲线L分别交于B,C两点。
(Ⅰ)以极点为原点,极轴为x轴的正半轴,取与极坐标相同单位长度,建立平面直角坐标系,写出曲线L和直线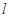 的普通方程;
的普通方程;
(Ⅱ)求|BC|的长。
设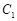 是以
是以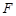 为焦点的抛物线
为焦点的抛物线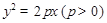 ,
,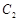 是以直线
是以直线 与
与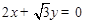 为渐近线,以
为渐近线,以 为一个焦点的双曲线.
为一个焦点的双曲线.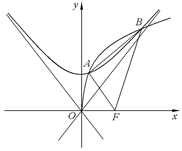
(1)求双曲线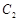 的标准方程;
的标准方程;
(2)若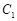 与
与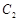 在第一象限内有两个公共点
在第一象限内有两个公共点 和
和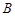 ,求
,求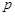 的取值范围,并求
的取值范围,并求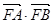 的最大值;
的最大值;
(3)若 的面积
的面积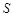 满足
满足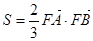 ,求
,求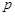 的值.
的值.
如图所示,质点P在正方形ABCD的四个顶点上按逆时针方向前进.现在投掷一个质地均匀、每个面上标有一个数字的正方体玩具,它的六个面上分别写有两个1、两个2、两个3一共六个数字.质点P从A点出发,规则如下:当正方体上底面出现的数字是1,质点P前进一步(如由A到B);当正方体上底面出现的数字是2,质点P前进两步(如由A到C),当正方体上底面出现的数字是3,质点P前进三步(如由A到D).在质点P转一圈之前连续投掷,若超过一圈,则投掷终止.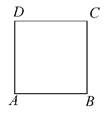
(1)求质点P恰好返回到A点的概率;
(2)在质点P转一圈恰能返回到A点的所有结果中,用随机变量ξ表示点P恰能返回到A点的投掷次数,求ξ的数学期望.
试题篮
()