如图,已知椭圆O: +y2=1的右焦点为F,点B,C分别是椭圆O的上、下顶点,点P是直线l:y=-2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.
+y2=1的右焦点为F,点B,C分别是椭圆O的上、下顶点,点P是直线l:y=-2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.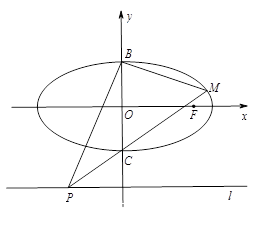
(1)当直线PM过椭圆的右焦点F时,求△FBM的面积;
(2)①记直线BM,BP的斜率分别为k1,k2,求证:k1·k2为定值;
②求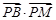 的取值范围.
的取值范围.
图1是一段半圆柱形水渠的直观图,其横断面如图2所示,其中C为半圆弧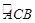 的中点,渠宽AB为2米.
的中点,渠宽AB为2米.
(1)当渠中水深CD为0.4米时,求水面的宽度;
(2)若把这条水渠改挖(不准填土)成横断面为等腰梯形的水渠,且使渠的底面与地面平行,则当改挖后的水渠底宽为多少时,所挖出的土量最少?
如图,在平面直角坐标系 中,设点
中,设点 是椭圆
是椭圆 上一点,从原点
上一点,从原点 向圆
向圆 作两条切线分别与椭圆
作两条切线分别与椭圆 交于点
交于点 ,直线
,直线 的斜率分别记为
的斜率分别记为 .
.
(1)若圆 与
与 轴相切于椭圆
轴相切于椭圆 的右焦点,求圆
的右焦点,求圆 的方程;
的方程;
(2)若 .
.
①求证: ;
;
②求 的最大值
的最大值
如图所示, 是两个垃圾中转站,
是两个垃圾中转站, 在
在 的正东方向
的正东方向 千米处,
千米处, 的南面为居民生活区. 为了妥善处理生活垃圾,政府决定在
的南面为居民生活区. 为了妥善处理生活垃圾,政府决定在 的北面建一个垃圾发电厂
的北面建一个垃圾发电厂 . 垃圾发电厂
. 垃圾发电厂 的选址拟满足以下两个要求(
的选址拟满足以下两个要求( 可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点
可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点 到直线
到直线 的距离要尽可能大). 现估测得
的距离要尽可能大). 现估测得 两个中转站每天集中的生活垃圾量分别约为
两个中转站每天集中的生活垃圾量分别约为 吨和
吨和 吨,问垃圾发电厂该如何选址才能同时满足上述要求?
吨,问垃圾发电厂该如何选址才能同时满足上述要求?
已知抛物线 过点
过点 .
.
(1)求抛物线 的方程;
的方程;
(2)是否存在平行于 (
( 为坐标原点)的直线
为坐标原点)的直线 ,使得直线
,使得直线 与抛物线
与抛物线 有公共点,且直线
有公共点,且直线 与
与 的距离为
的距离为 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
已知圆 ,直线
,直线 .
.
(1)求证:对任意 ,直线
,直线 与圆
与圆 总有两个不同的交点;
总有两个不同的交点;
(2)设直线 与圆
与圆 交于
交于 两点,若
两点,若 ,求直线
,求直线 的倾斜角.
的倾斜角.
如图,在平面直角坐标系 中,点
中,点 ,直线
,直线 ,设圆
,设圆 的半径为
的半径为 ,圆心在
,圆心在 上。
上。
(1)若圆心 也在直线
也在直线 上,过点
上,过点 作圆
作圆 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆 上存在点
上存在点 ,使
,使 ,求圆心
,求圆心 的横坐标
的横坐标 的取值范围.
的取值范围.
如图,三棱柱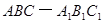 中,
中,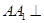 平面ABC,AB
平面ABC,AB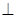 BC , 点M , N分别为A1C1与A1B的中点.
BC , 点M , N分别为A1C1与A1B的中点.
(Ⅰ)求证:MN 平面BCC1B1;
平面BCC1B1;
(Ⅱ)求证:平面A1BC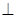 平面A1ABB1.
平面A1ABB1.
数列 为公差不为
为公差不为 的等差数列,
的等差数列, 为前
为前 项和,
项和, 和
和 的等差中项为
的等差中项为 ,且
,且 .令
.令 数列
数列 的前
的前 项和为
项和为 .
.
(Ⅰ)求 及
及 ;
;
(Ⅱ)是否存在正整数 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
试题篮
()