高中数学解答题

（本小题满分10分）选修4-4：坐标系与参数方程
已知在平面直角坐标系内，点 在曲线C：为参数，)上运动．以为极轴建立极坐标系，直线的极坐标方程为．
(Ⅰ) 写出曲线C的标准方程和直线的直角坐标方程；
(Ⅱ) 若直线与曲线C相交于A、B两点，点M在曲线C上移动，试求面积的
最大值．

如图，AB是圆O的直径，C是半径OB的中点，D是OB延长线上一点，且BD=OB，直线MD与圆O相交于点M、T（不与A、B重合），DN与圆O相切于点N，连结MC，MB，OT．
(1) 求证：；
(2) 若，试求的大小．

如图，在直三棱柱中，，是棱上的动点，是中点，，.
（Ⅰ）求证：平面；
（Ⅱ）若二面角的大小是，求的长.

按照新课程的要求, 高中学生在每学期都要至少参加一次社会实践活动(以下简称活动). 某校高一·一班50名学生在上学期参加活动的次数统计如条形图所示.

（I） 求该班学生参加活动的人均次数；
（II）从该班中任意选两名学生，求他们参加活动
次数恰好相等的概率；
（III）从该班中任选两名学生，用表示这两人参
加活动次数之差的绝对值，求随机变量的分布列及数学期望.（要求：答案用最简分数表示）学

（本小题满分12分）在中，分别为角的对边，且满足
（Ⅰ）求角的大小；
（Ⅱ）若，求的最小值．

若函数f（x）=在[1，+∞上为增函数.
（Ⅰ）求正实数a的取值范围.
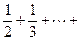
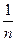
（Ⅱ）若a=1，求征：（n∈N*且n ≥ 2 ）

已知圆上的动点，点Q在NP上，点G在MP上，且满足.
（I）求点G的轨迹C的方程；
（II）过点（2，0）作直线l，与曲线C交于A、B两点，O是坐标原点，设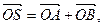 是否存在这样的直线l，使四边形OASB的对角线相等（即|OS|=|AB|）？若存在，求出直线l的方程；若不存在，试说明理由.

（3）（本小题满分7分）选修4-5；不等式选讲
若不等式，对满足的一切实数恒成立，求实数的取值范围。

（2）（本小题满分7分）选修4-4；坐标系与参数方程
过点且倾斜角为的直线和曲线：（为参数）相交于两点，求线段的长。

二阶矩阵对应的变换将向量，分别变换成向量，，直线 在的变换下所得到的直线的方程是，求直线的方程。

定义，，
（Ⅰ）令函数的图象为曲线，曲线与轴交于点，过坐标原点向曲线作切线，切点为，设曲线在点之间的曲线段与线段所围成图形的面积为，求的值；
（Ⅱ）令函数的图象为曲线，若存在实数使得曲线在处有斜率为-8的切线，求实数的取值范围；
（Ⅲ）当 且时，证明。

已知抛物线的顶点为坐标原点，椭圆的对称轴是坐标轴，抛物线在轴上的焦点恰好是椭圆的焦点
（Ⅰ）若抛物线和椭圆都经过点,求抛物线和椭圆的方程；
（Ⅱ）已知动直线过点，交抛物线于两点，直线：被以为直径的圆截得的弦长为定值，求抛物线的方程；
（Ⅲ）在（Ⅱ）的条件下，分别过的抛物线的两条切线的交点的轨迹为,直线与轨迹交于点,求的最小值。

如图，为圆的直径，点在圆上，
已知∥,,
,。
直角梯形所在平面与圆所在平面互相垂直。（Ⅰ）求证：平面平面；
（Ⅱ）求平面与平面所成角的余弦值；
（Ⅲ）在上是否存在一点,使∥平面?
若不存在，请说明理由;若存在，请找出这一点，并证明之

三角形的三个内角、、的对边的长分别为、、，有下列两个条件：（Ⅰ）、、成等差数列；（Ⅱ）、、成等比数列。
现给出三个结论：
①；②；③．
请你选取给定的两个条件中的一个条件为条件，三个结论中的两个为结论，组建一个你认为正确的命题，并证明之

为从甲、乙两名运动员中选拔一人参加2010年广州亚运会跳水项目，对甲、乙两名运动员进行培训．现分别从他们在培训期间参加的若干次预赛成绩中随机抽取6次,得出茎叶图如图所示
（Ⅰ）从平均成绩及发挥稳定性的角度考虑,你认为选派哪名运动员合适?
（Ⅱ）若将频率视为概率,对甲运动员在今后3次比赛成绩进行预测,记这3次成绩中高于80分的次数为,求的分布列及数学期望。