高中数学解答题

（本小题10分）口袋中有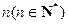个白球，3个红球．依次从口袋中任取一球，如果取到红球，那么继续取球，且取出的红球不放回；如果取到白球，就停止取球．记取球的次数为X．若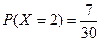，求：
（1）n的值；
（2）X的概率分布与数学期望．

[选做题]
A．选修4—1：几何证明选讲
如图，设AB为⊙O的任一条不与直线l垂直的直径，P是⊙O与l的公共点，AC⊥l，BD⊥l，垂足分别为C，D，且PC=PD，求证：
（1）l是⊙O的切线；
（2）PB平分∠ABD．

20090602

B．选修4—2：矩阵与变换
二阶矩阵 对应的变换将点 与 分别变换成点 与 ．求矩阵 ；
C．选修4—4：坐标系与参数方程
若两条曲线的极坐标方程分别为=l与=2cos(θ+)，它们相交于A，B两点，求线
段AB的长．
D．选修4—5：不等式选讲
求函数 的最大值．

设、．
（1）若在上不单调，求的取值范围；
（2）若对一切恒成立，求证：；
（3）若对一切，有，且的最大值为1，求、满足的条件．

已知等比数列的前项和为，且点在函数的图象上．
（1）求的值；
（2）若数列满足：，且．求数列的通项公式．

如图，已知圆交轴于、两点，在圆上运动（不与、重合），过作直线，垂直于交直线于点．
（1）求证：“如果直线过点，那么”为真命题；
（2）写出（1）中命题的逆命题，判断它是真命题还是假命题，并说明理由．

如图，棱柱ABCD-A₁B₁C₁D₁的底面ABCD为菱形，平面AA₁C₁C⊥平面ABCD．
（1）证明：BD⊥AA₁；
（2）证明：平面AB₁C//平面DA₁C₁
（3）在直线CC₁上是否存在点P，使BP//平面DA₁C₁？若存在，求出点P的位置；若不存在，说明理由．

已知向量，，设函数．
（1）求函数的最大值；
（2）在锐角三角形中，角、、的对边分别为、、，，且的面积为3，，求的值．

某校从参加高一年级期中考试的学生中随机抽取名学生，将其数学成绩（均为整数）分成六段，…后得到如下部分频率分布直方图，观察图形的信息，回答下列问题：
(Ⅰ)求分数在内的频率，并补全这个频率分布直方图；
(Ⅱ）统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计本次考试的平均分；
(Ⅲ）用分层抽样的方法在分数段为的学生中抽取一个容量为的样本，将该样本看成一个总体，从中任取人，求至多有人在分数段的概率.

已知为的三内角，且其对边分别为若
且
(Ⅰ)求角 
(Ⅱ)若的面积为求

设各项为正的数列满足：令

(Ⅰ)求
(Ⅱ)求证：

已知曲线上任意一点到点的距离比它到直线的距离小1.
(Ⅰ)求曲线的方程；
(Ⅱ)直线与曲线相交于两点，设直线的斜率分别为
求证：为定值.

已知函数，其中，为实常数且
(Ⅰ)求的单调增区间；
(Ⅱ)若对任意恒成立，求实数的取值范围.

如题18图，已知四棱锥的底面是边长为2的正方形，面分别为的中点.
(Ⅰ)求直线与面所成的角；
(Ⅱ)求二面角的大小.

在一次数学考试中，共有10道选择题，每题均有四个选项，其中有且只有一个选项是正确的，评分标准规定：“每道题只选一个选项，答对得5分，不答或答错得零分”.某考生已确定有6道题是正确的，其余题目中：有两道题可判断两个选项是错误的，有一道可判断一个选项是错误的，还有一道因不理解题意只好乱猜，请求出该考生：
(Ⅰ)得50分的概率；
(Ⅱ)设该考生所得分数为，求的数学期望.

关于的不等式
(Ⅰ) 当时，解不等式；
(Ⅱ)设函数，当为何值时，恒成立？