(本小题满分10分) 已知函数f(x)=|x-a|
(1)若不等式f(x)≤3的解集为[-1,5],求实数a的值.
(2)在(1)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.
(本小题满分10分)已知曲线C的参数方程为 (
( 为参数),
为参数),
以直角坐标系原点为极点,Ox轴正半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程;
(2)若直线 的极坐标方程为
的极坐标方程为 (sinθ+cosθ)=1,求直线
(sinθ+cosθ)=1,求直线 被曲线C截得的弦长.
被曲线C截得的弦长.
(本小题满分12分)已知函数f(x)=alnx ax
ax 3(a∈R).
3(a∈R).
(1)求f(x)的单调区间;
(2)设a=-1,求证:当x∈(1,+∞)时,f(x)+2>0;
(3)求证: ·
· ·
· ……
…… <
< (n∈N+且n≥2).
(n∈N+且n≥2).
(本小题满分12分)椭圆 +
+ =1(a>b>0)的左、右焦点为F1、F2,离心率为
=1(a>b>0)的左、右焦点为F1、F2,离心率为 ,过点F1的直线
,过点F1的直线 交椭圆于A、B两点,△AF2B的周长为8.
交椭圆于A、B两点,△AF2B的周长为8.
(1)求椭圆方程;
(2)若椭圆的左、右顶点为C、D,四边形ABCD的面积为 ,求直线
,求直线 的方程.
的方程.
(本小题满分12分)如图,在底面为菱形ABCD的四棱柱ABCD—A1B1C1D1 中,∠ABC=60°,AA1=AB=2,A1B=A1D=2 .
.
(1)求证:AA1⊥面ABCD;
(2)若点E在A1D上,且 =2,求二面角E—AC—D.
=2,求二面角E—AC—D.
(本小题满分12分)某同学参加语、数、外三门课程的考试,设该同学语、数、外取得优秀成绩的概率分别为 ,m,n(m>n),设该同学三门课程都取得优秀成绩的概率为
,m,n(m>n),设该同学三门课程都取得优秀成绩的概率为 ,都未取得优秀成绩的概率为
,都未取得优秀成绩的概率为 ,且不同课程是否取得优秀成绩相互独立.
,且不同课程是否取得优秀成绩相互独立.
(1)求m,n;
(2)设X为该同学取得优秀成绩的课程门数,求EX.
(本小题满分12分)已知函数f(x)=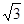 sin(x+
sin(x+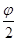 )cos(x+
)cos(x+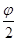 )+sin2(x+
)+sin2(x+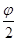 )(0<φ<
)(0<φ<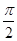 )的图象经过点(
)的图象经过点( ,1)
,1)
(1)求f(x);
(2)在△ABC中,A、B、C的对边为a、b、c,a= ,S△ABC=2
,S△ABC=2 ,角C为锐角且f(
,角C为锐角且f(

 )=
)= ,求c边长.
,求c边长.
(本小题满分10分)选修4-4:坐标系与参数方程
已知直线 的参数方程是
的参数方程是 ,圆C的极坐标方程为
,圆C的极坐标方程为 .
.
(1)求圆心C的直角坐标;
(2)由直线 上的点向圆C引切线,求切线长的最小值.
上的点向圆C引切线,求切线长的最小值.
(本小题满分10分)选修4-1:几何证明选讲
如图,⊙ 的直径
的直径 的延长线与弦
的延长线与弦 的延长线相交于点
的延长线相交于点 ,
, 为⊙
为⊙ 上一点,AE=AC ,
上一点,AE=AC , 交
交 于点
于点 ,且
,且 ,
,
(Ⅰ)求 的长度.
的长度.
(Ⅱ)若圆F与圆 内切,直线PT与圆F切于点T,求线段PT的长度
内切,直线PT与圆F切于点T,求线段PT的长度
已知椭圆 上的点到两焦点的距离和为
上的点到两焦点的距离和为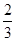 ,短轴长为
,短轴长为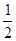 ,直线
,直线 与椭圆
与椭圆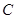 交于
交于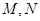 两点.
两点.
(Ⅰ)求椭圆C方程;
(Ⅱ)若直线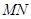 与圆
与圆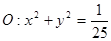 相切,证明:
相切,证明:  为定值;
为定值;
(Ⅲ)在(Ⅱ)的条件下,求 的取值范围.
的取值范围.
试题篮
()