高中数学解答题

（ 本小题满分12分） 在中，内角的对边分别为,且．已知,, ．求：
（1）的值；
（2）的值．

（本小题满分10分）选修4-5：不等式选讲
已知函数
（1） 解关于的不等式；
（2） 若函数的图象恒在函数图象的上方，求的取值范围．

（本小题满分10分）选修4－4：坐标系与参数方程
已知直线的参数方程是，圆C的极坐标方程为．
（1）求圆心C的直角坐标；
（2）由直线上的点向圆C引切线，求切线长的最小值．

（本小题满分10分）选修4-1：几何证明选讲
如图,⊙的直径的延长线与弦的延长线相交于点,为⊙上一点,AE＝AC ,交于点,且,

（Ⅰ）求的长度．
（Ⅱ）若圆F与圆内切，直线PT与圆F切于点T，求线段PT的长度

（本小题满分12分）已知函数
（1）若直线是曲线的切线，求的值；
（2）若直线是曲线的切线，求的最大值；
（3）设是曲线上相异三点，其中求证：

已知椭圆的离心率为,且过点,抛物线的焦点坐标为．
（1）求椭圆和抛物线的方程；
（2）若点是直线上的动点，过点作抛物线的两条切线，切点分别是，直线交椭圆于两点．

（Ⅰ）求证：直线过定点，并求出该定点的坐标；
（Ⅱ）当的面积取最大值时，求直线的方程．

已知四棱锥中，，，且底面是边长为1的正方形，是侧棱上的一点（如图所示）．

（1）如果点在线段上，，且，求的值；
（2）在（1）的条件下，求二面角的余弦值．

（ 本小题满分12分） 某高校在上学期依次举行了“法律、环保、交通”三次知识竞赛活动，要求每位同学至少参加一次活动．该高校2014级某班50名学生在上学期参加该项活动的次数统计如图所示

（1）从该班中任意选两名学生，求他们参加活动次数不相等的概率．
（2）从该班中任意选两名学生，用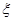表示这两人参加活动次数之差的绝对值，求随机变量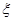的分布列及数学期望．
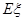（3）从该班中任意选两名学生，用表示这两人参加活动次数之和，记“函数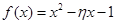在区间（3，5）上有且只有一个零点”为事件A，求事件A发生的概率．

（ 本小题满分12分） 在中，若，且，
（1）求角的大小；
（2）求的面积．

（本小题满分1 4分）已知椭圆的一个焦点与抛物线的焦点重合，且椭圆短轴的两个端点与
构成正三角形．
（1）求椭圆的方程：
（2）若过点的直线与椭圆交于不同两点，，试问在轴上是否存在定点，使
恒为定值？若存在，求出的坐标及定值；若不存在，请说明理由．

（本小题满分l3分）己知函数．
（1）求函数在点处的切线方程；
（2）若方程，在上有唯一零点，求实数的取值范围；
（3）对任意，恒成立，求实数的取值范闱．

（本小题满分1 2分）己知数列是各项均为正数的等差数列，其中，且，，构成等比数列：数列的前项和为，满足．
（1）求数列，的通项公式；
（2）如果，设数列的前项和为，是否存在正整数，使得成立，若存在，求出的最小值，若不存在，说明理由．

（本小题满分12分）如图在四棱锥中，底面是边长为的正方形，侧面底面，且，设，分别为，的中点．

（1）求证：平面；
（2）求证：面平面．

（本小题满分12分）已知高二某班学生语文与数学的学业永平测试成绩抽样统计如下表，若抽取学生人，成绩分为A（优秀）、B（良好）、C（及格）三个等级，设工，夕分别表示语文成绩与数学成绩，例如：表中语文成绩为B等级的共有20+18+4-42人，已知与均为B等级的概率是0．18．

（1）求抽取的学生人数；
（2）设该样本中，语文成绩优秀率是30%，求，的值；
（3）已知，，求语文成绩为A等级的总人数比语文成绩为C等级的总人数少的概率．

（本小题满分l 2分）在中，角，，的对边长分别是，，，且满足．
（1）求角的大小；
（2）若，的面积，试判断的形状，并说明理由．