如图,设椭圆 :
: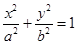
 的离心率
的离心率 ,顶点
,顶点 的距离为
的距离为 ,
,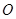 为坐标原点.
为坐标原点.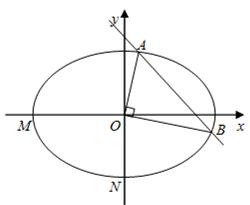
(1)求椭圆 的方程;
的方程;
(2)过点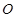 作两条互相垂直的射线,与椭圆
作两条互相垂直的射线,与椭圆 分别交于
分别交于 两点.
两点.
(ⅰ)试判断点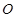 到直线
到直线 的距离是否为定值.若是请求出这个定值,若不是请说明理由;
的距离是否为定值.若是请求出这个定值,若不是请说明理由;
(ⅱ)求 的最小值.
的最小值.
己知椭圆C: (a>b>0)的右焦点为F(1,0),点A(2,0)在椭圆C上,过F点的直线
(a>b>0)的右焦点为F(1,0),点A(2,0)在椭圆C上,过F点的直线 与椭圆C交于不同两点
与椭圆C交于不同两点 .
.
(1)求椭圆C的方程;
(2)设直线 斜率为1,求线段
斜率为1,求线段 的长;
的长;
(3)设线段 的垂直平分线交
的垂直平分线交 轴于点P(0,y0),求
轴于点P(0,y0),求 的取值范围.
的取值范围.
已知椭圆 上的点
上的点 到左右两焦点
到左右两焦点 的距离之 和为
的距离之 和为 ,离心率为
,离心率为 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)过右焦点 的直线
的直线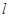 交椭圆于
交椭圆于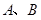 两点.
两点.
(1)若 轴上一点
轴上一点 满足
满足 ,求直线
,求直线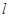 斜率
斜率 的值;
的值;
(2)是否存在这样的直线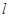 ,使
,使 的最大值为
的最大值为 (其中
(其中 为坐标原点)?若存在,求直线
为坐标原点)?若存在,求直线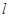 方程;若不存在,说明理由.
方程;若不存在,说明理由.
已知二次函数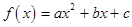 .
.
(1)若 ,试判断函数
,试判断函数 零点个数.
零点个数.
(2)若对 且
且 ,
, ,证明方程
,证明方程 必有一个实数根属于
必有一个实数根属于 .
.
(3)是否存在 ,使
,使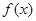 同时满足以下条件①当
同时满足以下条件①当 时,函数
时,函数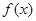 有最小值0;②对任意实数x,都有
有最小值0;②对任意实数x,都有 .若存在,求出
.若存在,求出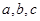 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
已知函数 (其中
(其中 且
且 ),
), 是
是 的反函数.
的反函数.
(1)已知关于 的方程
的方程 在
在 上有实数解,求实数
上有实数解,求实数 的取值范围;
的取值范围;
(2)当 时,讨论函数
时,讨论函数 的奇偶性和单调性;
的奇偶性和单调性;
(3)当 ,
, 时,关于
时,关于 的方程
的方程 有三个不同的实数解,求
有三个不同的实数解,求 的取值范围.
的取值范围.
对于定义域为 的函数
的函数 ,若同时满足下列条件:①
,若同时满足下列条件:①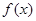 在
在 内单调递增或单调递减;②存在区间
内单调递增或单调递减;②存在区间 ,使
,使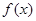 在
在 上的值域为
上的值域为 ;那么把
;那么把 (
( )叫闭函数,且条件②中的区间
)叫闭函数,且条件②中的区间 为
为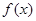 的一个“好区间”.
的一个“好区间”.
(1)求闭函数 的“好区间”;
的“好区间”;
(2)若 为闭函数
为闭函数 的“好区间”,求
的“好区间”,求 、
、 的值;
的值;
(3)判断函数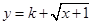 是否为闭函数?若是闭函数,求实数
是否为闭函数?若是闭函数,求实数 的取值范围.
的取值范围.
设 为奇函数,
为奇函数, 为常数.
为常数.
(Ⅰ)求 的值;
的值;
(Ⅱ)判断 在区间(1,+∞)的单调性,并说明理由;
在区间(1,+∞)的单调性,并说明理由;
(Ⅲ)若对于区间[3,4]上的每一个 值,不等式
值,不等式 >
> 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
试题篮
()