高中物理物体做曲线运动的条件计算题

我国已启动“嫦娥工程”，并于2007年10月24日和2010年10月1日分别将“嫦娥一号”和“嫦娥二号”成功发射。“嫦娥三号”亦有望在2013年落月探测90天，并已给落月点起了一个富有诗意的名字———“广寒宫”。
（1）若已知地球半径为R，地球表面的重力加速度为g，月球绕地球运动的周期为T，月球绕地球的运动近似看做匀速圆周运动，请求出月球绕地球运动的轨道半径r。
（2）若宇航员随登月飞船登陆月球后，在月球表面某处以速度v_o竖直向上抛出一个小球，经过时间t，小球落回抛出点。已知月球半径为r_月，引力常量为G，请求出月球的质量M

如图所示，飞机离地面高度为H＝500m，水平飞行速度为v₁＝100m/s，追击一辆速度为v₂＝20 m/s同向行驶的汽车，欲使炸弹击中汽车，飞机应在距离汽车的水平距离多远处投弹？(g=10m/s²)

25、在半径为R的某星球上，从高为h的平台上水平踢出一球，欲击中水平面上的A点，若两次踢球的方向都相同，第一次初速度为v1，着地点比A近了a，第二次初速度为v2，着地点却比A远了b，已知万有引力常量为G，求该星球的质量。

滚轴溜冰运动是青少年喜爱的一项活动。如图所示，一滚轴溜冰运动员（可视为质点）质量m=30kg，他在左侧平台上滑行一段距离后沿水平方向抛出，恰能无能量损失地从A点沿切线方向进入光滑竖直圆弧轨道并沿轨道下滑。已知A、B为圆弧的两端点，其连线水平；圆弧半径R="1.0" m，对应圆心角θ=106º；平台与A、B连线的高度差h="0.8" m。（取g=10m/s²，sin53º=0.80，cos53º=0.60）

求：（1）运动员做平抛运动的初速度；
（2）运动员运动到圆弧轨道最低点O时，对轨道的压力。

天文学家测得银河系中氦的含量约为25%。有关研究表明，宇宙中氦生成的途径有两条：一是在宇宙诞生后2分钟左右生成的；二是在宇宙演化到恒星诞生后，由恒星内部的氢核聚变反应生成的。
（1）4个氢核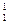（H）聚变成1个氦核（He），同时放出2个正电子（e）和2个中微子（ν₀），请写出该氢核聚变反应的方程，并计算一次反应释放的能量。
（2）研究表明，银河系的年龄约为t=3.8×10¹⁷s，每秒银河系产生的能量约为1×10³⁷J（P＝1×10³⁷J/s），现假定该能量全部来自上述氢核聚变反应，试估算银河系中氦的含量（最后结果保留2位有效数字）
（3）根据你的估算结果，对银河系中氦的主要生成途径作出判断。
　　（可能用到的数据：银河系的质量约为M＝3×10⁴¹kg，原子质量单位1u＝1.66×10kg，1u相当于1.5×10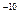J的能量，电子质量m_e＝0.0005u，氦核质量m_α＝4.0026u，氢核质量m_p＝1.0078u，中微子ν₀质量为零。

23、如图5所示，长为的轻杆OA绕O点在竖直平面内做匀速圆周运动，A端连着一个质量为的小球，取。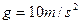
（1）如果小球的速度为3m/s，求在最低点时杆对小球的拉力为多大？
（2）如果在最高点杆对小球的支持力为4N，求杆旋转的角速度为多大？

已知万有引力常量G，地球半径R，月球与地球间距离r，同步卫星距地面的高度h，月球绕地球的运转周期T₁，地球自转周期T₂，地球表面的重力加速度g。某同学根据以上条件，提出一种估算地球质量M的方法：
同步卫星绕地心做圆周运动，由得
（1）请判断上面的结果是否正确，并说明理由。如不正确，请给出正确的解法和结果。
（2）请根据已知条件再提出一种估算地球质量的方法，并解得结果。

24、“神舟”五号载人飞船在绕地球飞行的第5 圈进行变轨，由原来的椭圆轨道变为距地面高度h的圆形轨道。已知地球半径R，地面处的重力加速度g ，试导出飞船在上述圆轨道上运行的周期T的公式（用h、R、g表示）。

如图所示，一根长=0.8m轻绳一端固定在O点，另一端栓一质量m=0.1kg的小球静止于A点，其右方有底面半径r=0.2m的转筒，转筒顶端与A等高，下部有一小孔，距顶端h=0.8m。现使细绳处于水平线上方30°的位置B点处而伸直，且与转筒的轴线、OA在同一竖直平面内，开始时小孔也在这一竖直平面内。将小球由B点静止释放，当小球经过A点时轻绳突然断掉，同时触动了光电装置，使转筒立刻以某一角速度匀速转动起来，且小球最终正好进入小孔。不计空气阻力，g取l0m/s²。试求：
（1）小球到达A点时的速率？
（2）转筒轴线距A点的距离L和转筒转动的角速度ω

如图是放置在竖直平面内游戏滑轨的模拟装置，滑轨由四部分粗细均匀的金属杆组成：水平直轨AB，半径分别为R₁ = 1.0m和R₂ = 3.0m的弧形轨道，倾斜直轨CD长为L = 6m，AB、CD与两圆形轨道相切，其中倾斜直轨CD部分表面粗糙，动摩擦因数为μ =，其余各部分表面光滑。一质量为m = 2kg的滑环（套在滑轨上），从AB的中点E处以v₀ = 10m/s的初速度水平向右运动。已知θ = 37°，（g取10m/s₂）求：
（1）滑环第一次通过O₂的最低点F处时对轨道的压力；
（2）滑环通过O₁最高点A的次数；
（3）滑环在CD段所通过的总路程。

半径为R的四分之一圆弧支架竖直放置，圆弧边缘C处有一小定滑轮，一根长度大于2R的轻绳两端系着质量分别为m₁、m₂的物体，挂在定滑轮两边，且m₁＞m₂，开始时m₁、m₂均静止，可视为质点，不计一切摩擦。试求：
（1）若m₁释放后一直沿圆弧轨道运动，求m₁经过圆弧最低点A时的速度；
（2）为使m₁能到达A点，m₁与m₂之间必须满足什么关系？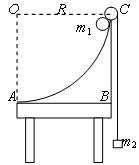

云室处在磁感应强度为B的匀强磁场中，一静止的质量为M的原子核在云室中发生一次α衰变，α粒子的质量为m，电量为q，其运动轨迹在与磁场垂直的平面内.现测得α粒子运动的轨道半径R，试求在衰变过程中的质量亏损.（注：涉及动量问题时，亏损的质量可忽略不计.）

在冬天，高为h=1.25m的平台上，覆盖了一层冰，一乘雪橇的滑雪爱好者，从距平台边缘s=24m处以一定的初速度向平台边缘滑去，如图所示，当他滑离平台即将着地时的瞬间，其速度方向与水平地面的夹角为θ=45°，取重力加速度g=10m/s²。求：

（1）滑雪者着地点到平台边缘的水平距离是多大；
（2）若平台上的冰面与雪橇间的动摩擦因数为μ=0.05，则滑雪者的初速度是多大？

如图所示，在水平固定的光滑平板上有一个质量为m的质点p，
由穿过中央小孔H的轻绳

20081027

一端连着。小孔是光滑的，用手拉着轻绳的

下端。使p做半径为r、角速度为ω₁的匀速圆周运动。若将 轻绳迅速
放松至某一长度R后再拉紧，质点就能在以半径为R的圆周上做匀速
圆周运动。则质点由半径r到R所需要的时间为          。质点在
半径为R的圆周上运动的角速度为          。

如图所示，竖直放置的光滑半圆形轨道与动摩擦因数为的水平面AB相切于B点，A、B两点相距L=2.5m，半圆形轨道的最高点为C，现将一质量为m=0.1kg的小球（可视为质点）以初速度v₀=9m/s沿AB轨道弹出，g=10m/s²。求

（1）小球到达B点时的速度大小及小球在A、B之间的运动时间；
（2）欲使小球能从最高点C水平抛出，则半圆形轨道的半径应满足怎样的设计要求？
（3）在满足上面（2）设计要求的前提下，半圆形轨道的半径为多大时可以让小球落到水平轨道上时离B点最远？最远距离是多少？