一辆汽车从原点O由静止出发沿x轴做直线运动，为研究汽车运动的规律而记录下它在不同时刻的位置和速度，见下表所示．试求：
| 时刻t/s |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 位置坐标x/m |
0 |
0.5 |
2 |
4.5 |
8 |
12 |
16 |
20 |
| 瞬时速度v/(m·s－1) |
0 |
1 |
2 |
3 |
4 |
4 |
4 |
4 |
（1）汽车在3.5 s末的速度；
（2）前4 s内的平均加速度．
动车把动力装置分散安装在每节车厢上.使其既具有牵引动力.又可以载客。而动车组就是几节自带动力的车辆（动车)加几节不带动力的车辆（也叫拖车）编成一组，若动车组在匀加速运动过程中.从计时开始，通过第一个60m所用时间是10s.通过第二个60m所用时间是6s.则（ ）
| A．动车组的加速度为0.5m/s2,接下来的6s内的位移为78m |
| B．动车组的加速度为1m/s2,接下来的6s内的位移为96m |
| C．动车组的加速度为0.5m/s2, 初速度为3.5m/s |
| D．动车组的加速度为lm/s2,前初速度为3.5m/s |
甲、乙两小分队进行代号为“猎狐”的军事演习，指挥部通过现代通信设备，在荧屏上观察到两小分队的具体行军路线如图所示．两小分队同时同地由O点出发，最后同时捕“狐”于A点．下列说法正确的是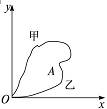
| A．小分队行军路程s甲＞s乙 |
| B．小分队平均速度v甲＝v乙 |
| C．小分队的平均速率相等 |
| D．图象表示的是位移—时间图象 |
一个质点做方向不变的直线运动，加速度的方向始终与速度方向相同，但加速度大小逐渐减小直至为零，则在此过程中（ ）
| A．速度逐渐增大，当加速度减小到零时，速度达到最大值 |
| B．速度逐渐减小，当加速度减小到零时，速度达到最小值 |
| C．位移逐渐增大，当加速度减小到零时，位移将不再增大 |
| D．位移逐渐减小，当加速度减小到零时，位移达到最小值 |
下列对各种速率和速度的说法中，正确的是（ ）
| A．平均速率就是平均速度 |
| B．瞬时速率是指瞬时速度的大小 |
| C．匀速运动中任意一段时间内的平均速度都等于其任一时刻的瞬时速度 |
| D．匀速直线运动中任何一段时间内的平均速度都相等 |
某中学身高1.7m，在学校运动会上参加跳高比赛，采用背越式，身体横着越过2.10m的横杆，获得了冠军，据此可估算出他起跳时竖直向上的速度约为（ ）
| A．9m/s | B．7m/s | C．5m/s | D．3m/s |
上午9时30分下课铃声响过之后，小李从教室到教师办公室去取作业本，沿直线走了60m，用了1分钟的时间．下列说法正确的是（ ）
| A．题中的“9时30分”是指时间 |
| B．题中的“1分钟”是指时刻 |
| C．小李的平均速度大小是1m/s |
| D．小李的平均速度大小是60m/s |
鸵鸟是当今世界上最大的鸟。有人说它不会飞是因为翅膀退化了，如果鸵鸟长了一副与身体大小成比例的翅膀，它是否就能飞起来呢？这是一个使人极感兴趣的问题，试阅读下列材料并填写其中的空白处。
鸟飞翔的必要条件是空气的上举力F至少与体重G＝mg平衡，鸟扇动翅膀获得的上举力可表示为 
，式中S为鸟翅膀的面积，v为鸟飞行的速度，c是恒量，鸟类能飞起的条件是 
，即 
_________，取等号时的速率为临界速率。
我们作一个简单的几何相似性假设。设鸟的几何线度为 
，质量 
体积 
， 
，于是起飞的临界速率 
。燕子的滑翔速率最小大约为20 km/h，而鸵鸟的体长大约是燕子的25倍，从而跑动起飞的临界速率为________km/h，而实际上鸵鸟的奔跑速度大约只有40km/h，可见，鸵鸟是飞不起来的，我们在生活中还可以看到，像麻雀这样的小鸟，只需从枝头跳到空中，用翅膀拍打一两下，就可以飞起来。而像天鹅这样大的飞禽，则首先要沿着地面或水面奔跑一段才能起飞，这是因为_______，而天鹅的______。
如图所示为成都到绵阳的和谐号动车车厢内可实时显示相关信息的显示屏的照片，图中甲、乙两处的数据分别表示了两个物理量。下列说法中正确的是（ ）
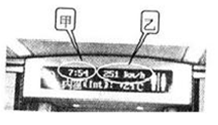
| A．甲处表示时刻，乙处表示瞬时速度 |
| B．甲处表示时间，乙处表示瞬时速度 |
| C．甲处表示时刻，乙处表示平均速度 |
| D．甲处表示时间，乙处表示平均速度 |
关于运动中速度、速度的变化量和加速度的关系，下列说法中不可能出现的是（ ）
| A．速度变化量的方向为正，加速度的方向为负。 |
| B．物体加速度增大，速度越来越小。 |
| C．速度变化越来越大，加速度反而越来越小。 |
| D．加速度与速度不在同一条直线上。 |
试题篮
()
粤公网安备 44130202000953号
