对于平面图形上的任意两点 , ,如果经过某种变换得到新图形上的对应点 , ,保持 ,我们把这种变换称为“等距变换”,下列变换中不一定是等距变换的是
A.平移B.旋转C.轴对称D.位似
某校为了解全校同学五一假期参加社团活动的情况,抽查了100名同学,统计它们假期参加社团活动的时间,绘成频数分布直方图(如图),则参加社团活动时间的中位数所在的范围是

A. 小时B. 小时C. 小时D.不能确定
如图,在 中, , ,分别以点 和点 为圆心,大于 的长为半径画弧,两弧相交于点 , ,作直线 ,交 于点 ,连接 ,则 的度数为
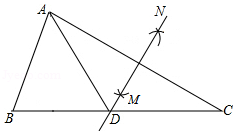
A. B. C. D.
下列说法正确的是
A.为了审核书稿中的错别字,选择抽样调查
B.为了了解春节联欢晚会的收视率,选择全面调查
C.“射击运动员射击一次,命中靶心”是随机事件
D.“经过有交通信号灯的路口,遇到红灯”是必然事件
2016年第一季度,我市“蓝天白云、繁星闪烁”天数持续增加,获得山东省环境空气质量生态补偿资金408万元,408万用科学记数法表示正确的是
A. B. C. D.
如图, 是 的角平分线,它的垂直平分线分别交 , , 于点 , , ,连接 , .
(1)请判断四边形 的形状,并说明理由;
(2)若 , , ,点 是 上的一个动点,求 的最小值.

星期天,李玉刚同学随爸爸妈妈回老家探望爷爷奶奶,爸爸 骑自行车先走,平均每小时骑行 ;李玉刚同学和妈妈 乘公交车后行,公交车平均速度是 .爸爸的骑行路线与李玉刚同学和妈妈的乘车路线相同,路程均为 .设爸爸骑行时间为 .
(1)请分别写出爸爸的骑行路程 、李玉刚同学和妈妈的乘车路程 与 之间的函数解析式,并注明自变量的取值范围;
(2)请在同一个平面直角坐标系中画出(1)中两个函数的图象;
(3)请回答谁先到达老家.
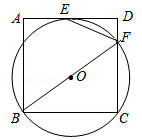
如图,过正方形 顶点 , 的 与 相切于点 ,与 相交于点 ,连接 .
(1)求证: 平分 .
(2)若 , ,求 的长.
某运动员在一场篮球比赛中的技术统计如表所示:
|
技术 |
上场时间(分钟) |
出手投篮(次) |
投中 (次) |
罚球得分 |
篮板 (个) |
助攻(次) |
个人总得分 |
|
数据 |
46 |
66 |
22 |
10 |
11 |
8 |
60 |
注:表中出手投篮次数和投中次数均不包括罚球.
根据以上信息,求本场比赛中该运动员投中2分球和3分球各几个.
试题篮
()