如图, 中, 为钝角, ,点 是边 延长线上一点,以点 为顶点, 为边,在射线 下方作 .
(1)在射线 上取点 ,连接 交线段 于点 .
①如图1,若 ,请直接写出线段 与 的数量关系和位置关系;
②如图2,若 ,判断线段 与 的数量关系和位置关系,并说明理由;
(2)如图3,反向延长射线 ,交射线 于点 ,将 沿 方向平移,使顶点 落在点 处,记平移后的 为 ,将 绕点 顺时针旋转角 , 交线段 于点 , 交射线 于点 ,请直接写出线段 , 与 之间的数量关系.

铁岭“荷花节”举办了为期15天的“荷花美食”厨艺秀.小张购进一批食材制作特色美食,每盒售价为50元,由于食材需要冷藏保存,导致成本逐日增加,第 天 且 为整数)时每盒成本为 元,已知 与 之间满足一次函数关系;第3天时,每盒成本为21元;第7天时,每盒成本为25元,每天的销售量为 盒, 与 之间的关系如下表所示:
|
第 天 |
|
|
|
每天的销售量 盒 |
10 |
|
(1)求 与 的函数关系式;
(2)若每天的销售利润为 元,求 与 的函数关系式,并求出第几天时当天的销售利润最大,最大销售利润是多少元?
(3)在“荷花美食”厨艺秀期间,共有多少天小张每天的销售利润不低于325元?请直接写出结果.
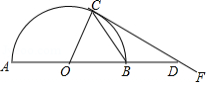
如图, 是半圆 的直径,点 是半圆上一点,连接 , ,以点 为顶点, 为边作 ,延长 交 于点 .
(1)求证:直线 是半圆 的切线;
(2)若 , ,求 的长.
如图,某市文化节期间,在景观湖中央搭建了一个舞台 ,在岸边搭建了三个看台 , , ,其中 , , 三点在同一条直线上,看台 , 到舞台 的距离相等,测得 , , ,小明、小丽分别在 , 看台观看演出,请分别求出小明、小丽与舞台 的距离.(结果保留根号)

某大型快递公司使用机器人进行包裹分拣,若甲机器人工作 ,乙机器人工作 ,一共可以分拣700件包裹;若甲机器人工作 ,乙机器人工作 ,一共可以分拣650件包裹.
(1)求甲、乙两机器人每小时各分拣多少件包裹;
(2)“双十一”期间,快递公司的业务量猛增,要让甲、乙两机器人每天分拣包裹的总数量不低于2250件,它们每天至少要一起工作多少小时?
某校九年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题中选择一个,九年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.

(1)求本次调查共抽取了多少名学生的征文;
(2)将上面的条形统计图和扇形统计图补充完整;
(3)如果该校九年级共有1200名学生,请估计选择以“友善”为主题的九年级学生有多少名;
(4)本次抽取的3份以“诚信”为主题的征文分别是小义、小玉和大力的,若从中随机选取2份以“诚信”为主题的征文进行交流,请用画树状图法或列表法求小义和小玉同学的征文同时被选中的概率.
如图, 的面积为 .点 , , , , 是边 的 等分点 ,且 为整数),点 , 分别在边 , 上,且 ,连接 , , , , ,连接 , , , , ,线段 与 相交于点 ,线段 与 相交于点 ,线段 与 相交于点 , ,线段 与 相交于点 ,则△ ,△ ,△ , ,△ 的面积和是 .(用含有 与 的式子表示)

如图,在圆心角为 的扇形 中,半径 ,点 , 为 的三等分点,连接 , , , , ,则图中阴影部分的面积为 .

如图,菱形 的面积为6,边 在 轴上,边 的中点 在 轴上,反比例函数 的图象经过顶点 ,则 的值为 .

学校准备从甲、乙、丙、丁四名同学中选择一名同学代表学校参加市里举办的“汉字听写”大赛,四名同学平时成绩的平均数 (单位:分)及方差 如下表所示:
|
甲 |
乙 |
丙 |
丁 |
|
|
|
94 |
98 |
98 |
96 |
|
|
1 |
1.2 |
1 |
1.8 |
如果要选出一个成绩好且状态稳定的同学参赛,那么应该选择的同学是 .
试题篮
()