初中数学有理数解答题

化简求值．
（1）化简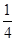：（-4a²+2a-8）-2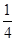（a-1）-1；
（2）化简求值：-a²b+3（3ab²-a²b）-2（2ab²-a²b），其中|a-1|+（b+2）²=0．

已知是最大的负整数，b是多项式的次数，c是单项式的系数，且、b、c分别是点A、B、C在数轴上对应的数．
（1）求、b、c的值，并在数轴上标出点A、B、C．

（2）若动点P、Q同时从A、B出发沿数轴负方向运动，点P的速度是每秒1个单位长度，点Q的速度是每秒个单位长度，求运动几秒后，点Q可以追上点P？
（3）在数轴上找一点M，使点M到A、B、C三点的距离之和等于12，请直接写出所有点M对应的数．（不必说明理由）．

若、互为相反数，、互为倒数，的绝对值等于2，计算的值。

为了有效控制酒后驾车，某市城管的汽车在一条东西方向的公路上巡逻，如果规定向东为正，向西为负，从出发点开始所走的路程为 ：+2，-3，+2，＋1，－2，－1，－2．（单位：千米）；
（1）此时，这辆城管的汽车司机如何向队长描述他的位置?
（2）如果队长命令他马上返回出发点，这次巡逻（含返回）共耗油多少升？（已知每千米耗油 0．2升）

如图：在数轴上A点表示数a，B点示数b，C点表示数c，b是最小的正整数，且a，c满足+（c－8）²=0．

（1）a =       ，b =       ，c =       ．
（2）若将数轴折叠，使得A点与B点重合，则点C与数       表示的点重合．
（3）点A，B，C开始在数轴上运动，若点A以每秒2个单位长度的速度向左运动，同时，点B和点C分别以每秒4个单位长度和8个单位长度的速度向右运动，假设t秒钟过后，若点A与点B之间的距离表示为AB，点A与点C之间的距离表示为AC，点B与点C之间的距离表示为BC．则AB =       ，AC =       ，BC =       ．（用含t的代数式表示）
（4）请问：3AB－（2BC+AC）的值是否随着时间t的变化而改变? 若变化，请说明理由；若不变，请求其值．

某检修小组从A地出发，在东西向的马路上检修线路，如果规定向东行驶为正，向西行驶为负，一天中七次行驶记录如下．（单位：km）

第一次	第二次	第三次	第四次	第五次	第六次	第七次
－4	＋7	－9	＋10	＋6	－5	－6

 
（1）求收工时，检修小组在A地的哪个方向？距离A地多远？
（2）在第几次记录时距A地最近？
（3）若汽车行驶每千米耗油0．2升，问从A地出发，检修结束后再回到A地共耗油多少升？

某班10名男同学参加100米达标测验，成绩小于或等于15秒的达标，这10名男同学成绩记录如下（其中超过15秒记为“+”，不足15秒记为“－”）：
+1．2，0，－0．8，+2，0，－1．4，－0．5，0，－0．3，+0．8
（1）求这10名男同学的达标率是多少？（“达标率”是指达标人数占参加人数的百分比）
（2）这10名男同学的平均成绩是多少？
（3）最快的比最慢的快了多少秒？

化简求值
（1）先化简再求值：，其中．
（2）有理数a，b，c在数轴上的位置如图所示，请化简：．

（3）若A=，B=，请计算：3A−2B，并求当x=1时这个代数式的值．

已知a是相反数等于它本身的数，b是最大的负整数,求代数式a³+3a²b+3ab²+b³的值。

计算：
（1）2015²-2016×2014                 
（2）（x⁴-2x²y²）÷x²-（x+y）²

已知a、b互为相反数，c、d互为倒数，．求的值．

用数轴上的点表示﹣3.5，，，4，0，2.5，再用“＜”把这些数连接起来．

出租车司机小李某天下午的营运全是在东西走向的人民大街上行驶的，如果规定向东为正，向西为负，他这天下午行车里程（单位：千米）如下：
+15，－2，+5，－1，+10，－3，－2，+12，+4，－5，+6．
（1）若小李下午出发地记为0，他将最后一名乘客送抵目的地时距出发地点有多远？
（2）若汽车耗油量为0.41升/ 千米，这天下午小李共耗油多少升？

观察下面的变形规律：
 ＝1－；＝－；＝－；……解答下面的问题：
（1）若n为正整数，请你猜想＝                   ；
（2）求和：＋＋．（注：只能用上述结论做才能给分）；
（3）用上述相似的方法求和：．

如图，某学校新建了一座吴玉章雕塑，小林站在距离雕塑2．7米的A处自B点看雕塑头顶D的仰角为45°，看雕塑底部C的仰角为30°，求塑像CD的高度．（最后结果精确到0．1米，参考数据：≈1．732）